本题易错项B,构造函数题,最常用的就是一次函数,二次函数和三角函数。我们构造的函数都是基本初等函数或者分段函数,优先考虑一次函数和二次函数,周期性的函数优先考虑三角函数。构造函数应充分利用定义域和值域的对应关系及其单调性、凹凸性。
例如对数函数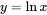 定义在
定义在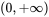 ,值域为
,值域为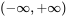 ,单调递增,上凸函数,熟悉基本初等函数的这些性质是构造函数题的基础。
,单调递增,上凸函数,熟悉基本初等函数的这些性质是构造函数题的基础。
构造分段函数就要分开构造,构造多个定义在不同定义域上的函数。
对于抽象函数,也是构造一个或多个特例来解决问题。
例如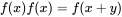 ,考虑指数函数和特例
,考虑指数函数和特例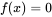 ,
,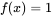 。
。
这种题有一定的发散性,需要尝试。

