|
反证法与放缩法
1、 反证法:
一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法。
一般直接证明较困难的,采用反证法,反证法是解决某些“疑难”问题的有力工具。所说的矛盾,通常是指推出的结果与已知公理、已知定义、已知定理或已知条件矛盾,与临时假设矛盾以及自相矛盾等各种情况。
应用反证法证明的一般步骤:反设——归谬——结论
在应用反证法证明时,必须按“反设——归谬——结论”的思路进行,这就是应用反证法的三步曲,但叙述上可以简略每一步的名称。
2、 放缩法
放缩法是不等式证明的基本方法,在不等式证明中几乎无处不见,它的依据是不等式的基本性质:若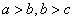 ,则 ,则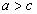 .一般可考虑利用添项、舍项、已知不等式及函数的单调性等将欲证不等式的左边或右边进行放大或缩小。 .一般可考虑利用添项、舍项、已知不等式及函数的单调性等将欲证不等式的左边或右边进行放大或缩小。
|

