|
②解不等式:
一元一次不等式、一元二次不等式是解不等式的基本点与基础,这里重点叙述利用不等式性质解不等式。
⑴高次不等式:把高次不等式因式分解,利用不等式的可乘性把高次不等式转化为一次或二次不等式,进而解之。
模型:
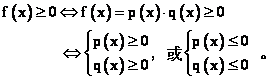
特殊地,f(x)能全部分解成一次因式,那用数轴标根法解之。

⑵分式不等式:利用不等式的可乘性把分式不等式两边同乘以分母的平方转化为整式不等式。
模型:
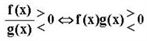
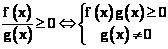 ,或 ,或 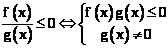 。 。
⑶无理不等式:利用不等式的乘方性把无理不等式两边平方转化为有理不等式。
模型:
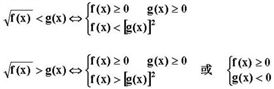
⑷绝对值不等式:
Ⅰ、绝对值的定义:
在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值。其性质为

Ⅱ、绝对值不等式性质:
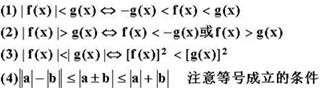
Ⅲ、解法原则:

Ⅳ、模型:
(1) 设a为正数。根据绝对值的意义,不等式
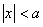
的解集是
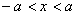
它的几何意义就是数轴上到原点的距离小于a的点的集合,如图,它是开区间(-a,a)。

(2) 设a为正数。根据绝对值的意义,不等式

的解集是
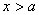 或 或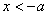 。 。
它的几何意义就是数轴上到原点的距离大于a的点的集合,如图,它是两个开区间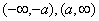 的并集。 的并集。

(3) 设a为正数,解不等式
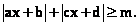
根据绝对值的意义,我们先求出ax+b和cx+d的零点,再分区间讨论。容易得出 分别是ax+b和cx+d的零点。它们把数轴分成三个区间 分别是ax+b和cx+d的零点。它们把数轴分成三个区间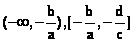 , ,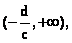 (不妨设 (不妨设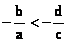 )即 )即

|

