|
直线与圆的方程的应用
①直线与圆方程建模:
直线与圆的方程在生产、生活实际以及数学中有着十分广泛的应用,它涉及到质量、重心、气象预报、购物选址、光的折射、直线型经验公式的选用等问题。
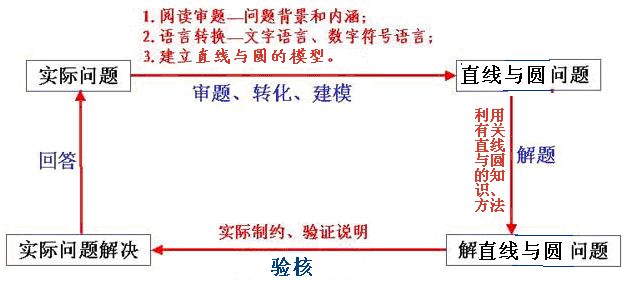
②坐标法解决几何问题:
坐标法或称解析法,即通过建立适当的平面直角坐标系,把几何问题代数化的方法。其步骤是:
Ⅰ、建立适当的平面直角坐标系,用坐标、方程表示问题中的几何元素,将平面几何问题转化为代数问题;
Ⅱ、通过代数运算,解决代数问题;
Ⅲ、将代数运算结果“翻译”成几何结论。
案例:已知圆内接四边形的对角线互相垂直,求证:圆心到一边的距离等于
这条边所对边长的一半。
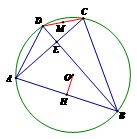
③几何法解决代数问题:
简称几何法,即通过建立的平面直角坐标系,把二元代数问题几何化的方法。
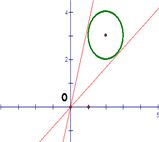
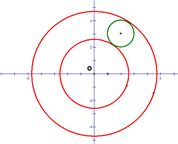
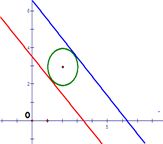
例如,已知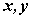 是实数,且 是实数,且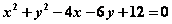 ,求(1) ,求(1)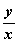 的最值;(2) 的最值;(2) 的最值;(3) 的最值;(3)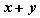 的最值。 的最值。
这里,把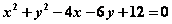 看成已知圆, 看成已知圆,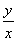 表示过原点的直线系与已知圆的位置关系,相切时达到最值; 表示过原点的直线系与已知圆的位置关系,相切时达到最值; 表示圆心在原点的同心圆系与已知圆的位置关系,相切时达到最值; 表示圆心在原点的同心圆系与已知圆的位置关系,相切时达到最值;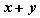 表示斜率为-1的平行直线系与已知圆的位置关系,相切时达到最值。 表示斜率为-1的平行直线系与已知圆的位置关系,相切时达到最值。
|

