A、问题情境

若已知三角形两角及一边或已知两边及其中一边的对角，都能通过正弦定理解这个三角形。那么，如果在一个三角形中已知两边和这两边的夹角，你能求这个三角形的第三条边吗？   

启发：

对一个直角三角形来说，它的斜边的平方等于两条直角边的平方和，那么对于任意一个三角形来说，是否也可以根据一个角和此角的两夹边，求此角的对边呢？

示范研究：

如图，RtΔABC中，∠C＝90^o，

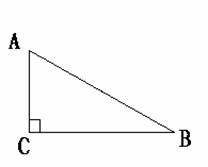
由勾股定理有，AB²=AC²+CB²。

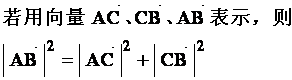
即 ，

思考：能否用同样的方法，由三角形的两边及夹角，求第三边呢？请动手试试。

如图，在ΔABC中，AB、BC、CA的长为c，a，b

由向量的加法得：

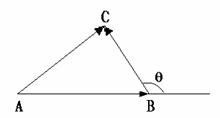
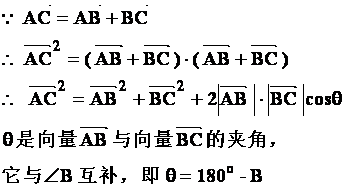
∴ cosθ=-cosB

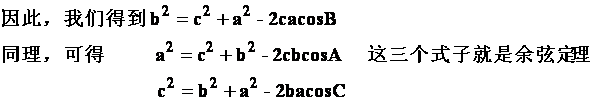
从而由余弦定理解决了由三角形的两边及夹角，求第三边的问题。

 

评注：

余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的积的两倍

（1）余弦定理揭示了三角形两边夹角和第三边的等量关系，知道其中三个量，可求第四个量。

（2）余弦定理中，若令C=90^o，则cosC=0。余弦定理变为勾股定理，因此勾股定理是余弦定理的特例，余弦定理是勾股定理的一般推广

（3）余弦定理的变形

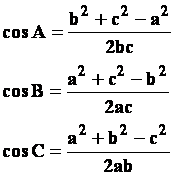
（4）利用余弦定理可以解决哪些类型的三角形问题？

①已知三角形三边求三个角

②已知两边和它们的夹角，求第三边及其余两个角