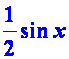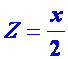A：问题情景
如何用“五点法”画函数y=Asinx(A>0,A≠1)与y=sinωx(ω>0, ω≠1)的简图，揭示A、ω对函数图像的影响。
分析示范
1、回顾“五点法”画函数y=sinx的简图
x
|
0 |
|
|
|
|
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
2、如何寻找关键的“五点”，画函数y=3sinx、y＝ 
sinx的简图。
x
|
0 |
|
|
|
|
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
3Sinx
|
0 |
3 |
0 |
-3 |
0 |
|
|
0 |
|
0 |
- |
0 |
3、如何寻找关键的“五点”，画函数y=sin2x、y＝sin x的简图。
x
|
0 |
|
|
|
|
Z=2x
|
0 |
|
|
|
|
|
SinZ |
0 |
1 |
0 |
-1 |
0 |
x
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
0 |
4、A、ω对函数图像的影响
（1）函数y=Asinx,
x∈R (A>0,A≠1)的图像，可以看作把正弦曲线上所有点的纵坐标伸长（当A>1）或缩短（当0<A<1）到原来的A倍（横坐标不变）而得到。函数y=Asinx, x∈R的值域是[-A, A]，A的物理意义是振动的振幅。
（2）函数y=sinωx, x∈R (ω>0, ω≠1)的图像，可以看作把正弦曲线上所有点的横坐标缩短（当ω>1）或伸长（当0<ω<1）到原来的
倍（纵坐标不变）而得到。函数y=sinωx,x∈R的周期是T=
：ω决定着振动的频率f,f=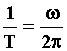
.
