相关链接A

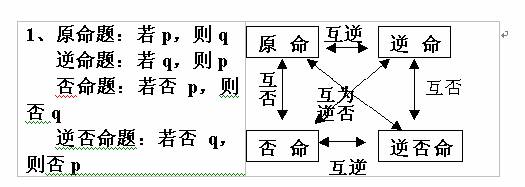
2、从图上看，横向互逆，纵向互否，交叉互为逆否。

相关链接B

准确理解四种命题的相互关系

（1） 四种命题是相对而言的，一经指定一个命题是原命题后，这一命题的
逆命题、否命题和逆否命题就被确定，当改变原命题时，则其他三个命题
也随之改变。

如：设“若x>3，则x>1”为原命题，
则它的逆命题是“若x>1，则x>3”，
否命题是“若x≤3，则x≤1”，
逆否命题是“若x≤1，则x≤3”
但当以“若x≤3，则x≤1”为原命题时，
则它的逆命题是“若x≤1，则x≤3”，
否命题是“若x>3，则x>1”，
逆否命题是“若x>1，则x>3”

（2） 两个等价关系不变，即不论以哪一种形式的命题为原命题，

原命题与它的逆否命题，原命题的逆命题与原命题的否命题都是等价命题。
从本质上看，即当一个命题的条件和结论与另一个命题的结论和条件刚好
相互否定时，这两个命题一定是等价的，它们具有相同的真假。基于这一
点，在证明命题时常可采用变更命题的技巧性手法，欲证一个命题，可以
构造它的逆否命题，改证它的逆否命题。

（3）一个命题的否定应当包含除了本身以外的所有情况。

　　  如：“都相等”的否定应为“不都相等”，即至少有两个元素不相等。
“p或q”与“┐p且┐q”互为否定；“一定是”的否定是“一定不是”。