A、问题情境
思考：
两条异面直线的公垂线有几条？为什么？
示范
结论：任意两条异面直线有且只有一条公垂线。
（1）存在性：
如图，设a、b是两条异面直线，在b上取一点P，过点P作a,∥a，
∵ 
，则b与a,可以确定一个平面，设为α，
∴ a∥α。
在a上任取一点Q，作QM⊥α于点M，
∵ 
，则a与QM确定一个平面，设为β，且
，
则b与c必相交于一点B（否则b∥c与a、b是异面直线矛盾）。
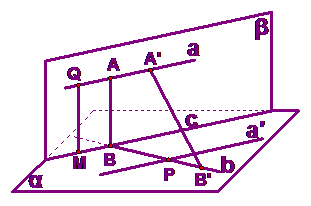在β内作BA∥MQ，交a于点A，则
AB⊥α，又
，
∴ AB⊥b，AB⊥a,，
又a∥a,，
∴ AB⊥a，
∴ AB,是异面直线a、b的公垂线。
（2）唯一性：
假设还有直线A,B,也是异面直线a、b的公垂线，则
A,B,⊥b，A,B,⊥a，
∵a∥a,，∴A,B,⊥a,，又a,∩a=P
∴A,B,⊥α，又AB⊥α
∴A,B,∥AB
∴A,B,、AB共面，于是a、b共面，这与a、b是异面直线相矛盾。
∴假设错误，因此两条异面直线的公垂线只有一条。
3、异面直线除上述性质外，还有哪些性质？请从“距离”意义的角度思考。
