A、问题情境

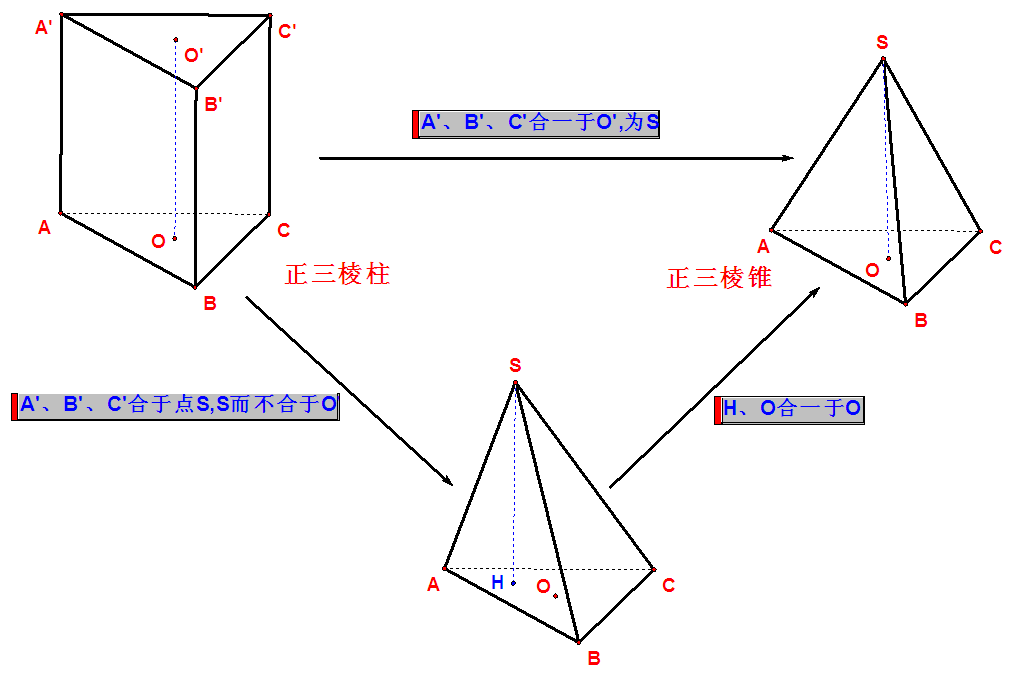
   3、学习过正棱柱，联想何谓正棱锥(若联想不出，可以看书)？依此定义，想象正棱锥应具有哪些性质(若想象能力不足，可以通过实物观察，或看书帮助)？为什么？

   示范   演示

   (1)画图想象(以三棱锥为例)正棱锥定义：

   正棱锥：底面是正多边形，顶点在底面的射影是底面中心的棱锥。

   (2)正棱锥具有的性质(以三棱锥为例)：

    ①   

       又 AB=BC=CA    

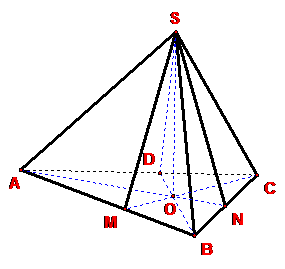
       ∴ △SAB≌△SBC≌△SCA       

       ∴ SM=SN=SD(称为斜高)。

       所以，正棱锥的侧棱相等，侧面是全等的等腰三角形，斜高相等。

② SO⊥底面ABC

∴ ∠SAO、∠SBO、∠SCO是侧棱与底面所成的角 ，且∠SAO=∠SBO=∠SCO。

   SO⊥底面ABC

       OM⊥AB、ON⊥BC、OD⊥CA      

SM⊥AB、SN⊥BC、SD⊥CA，

∴∠SMO、∠SNO、∠SDO是侧面与底面所成二面角的平面角 ，且∠SMO=∠SNO=∠SDO。

所以，正棱锥侧棱与底面所成的角相等，侧面与底面所成的二面角相等 。

③ 设正棱锥侧棱为l，高为h，斜高为h´，则

   在Rt△SOA中，l²=h²+R² (R是多边形外接圆半径)；

  在Rt△SOM中，l´²=h²+r²是多边形内切圆半径)；

  所以，正棱锥的高、侧棱、侧棱在底面内的射影(即底面正多边形外接圆的半径)组成一个直角三角形；正棱锥的高、斜高、斜高在底面内的射影(即底面正多边形的内切圆的半径)组成一个直角三角形。