第十四章 导数学习的形成性评价(1)
一、选择题(每小题5分，共60分)
1、设f(x)=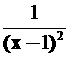
，则f
(0)等于(
)
A.-2 B.
2、曲线y=
x5+3x2+4x在x=-1处的切线的倾斜角是( )
A.-
B.
C.
D.
3、设y=e-x，则y等于( )
A.y=ex B.e-x
C.-e-x
D.-e-x
4、已知曲线y=x2+2x-3在点M处的切线与x轴平行，则点M的坐标是( )
A.(-1，4) B.(-1，-4) C.(-2，-4) D.(-2，4)
5、下列函数中，在(0，+∞)内为增函数的是( )
A.sin2x B.xex C.x3-x D.-x+ln(1+x)
6、f(x)=xa-ax(0＜a＜1)，则f(x)在[0，+∞)内的极大值点x0等于( )
A.0 B.a C.1 D.1-a
7、函数y=x3-3x在区间( )
A.(-1，1)内是单调增函数
B.(-1，1)内是单调减函数
C.(-∞，-1)及(1，+∞)内均为单调减函数
D.(-∞，-1)内是单调增函数，(1，+∞)内是单调减函数
8、三次函数当x=1时有极大值4，当x=3时有极小值0，且函数过原点，则此函数是( )
A.y=x3+6x2+9x B.y=x3-6x2+9x
C.y=x3-6x2-9x
D.y=x3+6x2-9x
9、若正方体的棱长从
10、函数y=lgx( )
A.有最大值，无最小值 B.无最大值，有最小值
C.有最大值和最小值 D.无最大值和最小值
11、点P在曲线y=x3-x+
上移动时，过点P的切线的倾斜角的取值范围是( )
A.[0，π] B.(0，
)∪[，π)
C.[0，]∪[，] D.[0，]∪[，π)
12、若曲线y=f(x)在点(x0，f(x0))处的切线方程为2x-y+1=0，则( )
A.f(x0)＞0
B.f(x0)＜(x0)=0 D.f(x0)不存在
二、填空题(每小题4分，共16分)
13、函数y=sinx·cosx的导数为
14、函数f(x)=
在x=2处的导数值为
，则a=
15、f(x)=x(x-c)2在x=2处有极大值，则常数c的值为
16、将长为l的铁丝剪成两段，各围成长与宽之比为2:1及3:2的矩形，那么面积之和的最小值为
三、解答题(本大题共6小题，共74分)
17、(12分)求过曲线y=cosx上点P(
，
)且与过这点的切线垂直的直线方程.
18、(12分)已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间；
(2)若f(z)在区间[-2，2]上的最大值为20，求它在该区间上的最小值.
19、(12分)设a为实数，函数f(x)=x3-x2-x+a.
(1)求f(x)的极值；
(2)当a在什么范围内取值时，曲线y=f(x)与x轴仅有一个交点.
20、(12分)已知函数f(x)=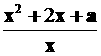 
，x∈[1，+∞).
(1)当a=时，求函数f(x)的最小值；
(2)若对任意x∈[1，+∞)，f(x)＞0恒成立，试求实数a的取值范围.
21、(12分)欲设计一容积为V的有盖圆柱形的饮料筒，已知侧面积的单位面积的造价是底面积单位面积造价的一半，而盖的单位面积的造价又为侧面积单位面积造价的一半，问此筒的半径r和高h之比为何值时，其造价最省?
22、(14分)设函数f(x)= 
(其中λ＞0)，求λ的取值范围，使函数f(x)在区间[0，+∞)上是单调减函数.
第三章 单元综合测评 参考答案
一、选择题
1、D 2、C 3、D 4、B 5、B 6、C 7、B 8、B 9、A 10、D 11、D 12、A
二、填空题
13、cos2x 14、2或
15、6 16、
l2
三、解答题
17、2x-
y-
+
=0
18、(1)函数f(x)的单调递减区间为(-∞，-1)、(3，+∞)
(2)f(2)和f(-1)分别是f(x)在区间[-2，2]上的最大值和最小值.
所以(-1)=1+
19、(1)
所以，f(z)的极大值是f(-
)=
+a，极小值是f(1)=a-1.
(2)a∈(-∞，-)∪(1，+∞)时，曲线y=f(x)与x轴仅有一个交点.
20、(1)函数f(x)在[1，+∞)上的最小值为f(1)=
.
(2)当a＞-3时，对任意x∈[1，+∞)，f(x)＞0恒成立.
21、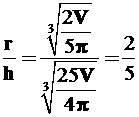
时，饮料桶的造价最省
22、当∈[1，+∞)，函数f(x)在区间[0，+∞)上是单调减函数
