第十二章 概率与统计 单元形成性评价

一、选择题(每小题5分，计60分)

1.描述总体离散程序或稳定性的特征数是总体方差σ²，以下统计量能估计总体稳定性的有(    )

A.样本值差         B.样本方差S²

C.样本最大值x_(n)        D.样本最小值x₍₁₎

解析：本题考查样本均值、样本方差的概念及其对总体特征的相应估计。样本方差估计的是总体方差(样本标准差估计的是总体标准差)，样本均值估计的是总体平均水平.方差越大，说明总体相对集中性稳定性较差.反之总体稳定性强，相对集中程度高。样本方差S²可估计总体方差，故应选B。

答案：B

2.设随机变量ξ的分布列为：P(ξ=k)=a (k=0，1，2，…)λ>0(常数)，则a等于(    )

A.2e^－λ             B.e^λ           C.e^－λ           D.3e^－λ

解析：∵，∴。

从而a=e^－λ。

答案：C

3.设P(ξ=±1)=，则σ(2ξ+5)等于(    )

A.2            B.4         C.1           D.6

解析：∵P(ξ=±1)= ，∴Eξ=0。

Eξ²=1，∴Dξ=1，D(2ξ+5)=2²·Dξ=4，

∴σ(2ξ+5)=2，故选A。

答案：A

4.设随机变量ξ的分布列为P(ξ=i)=，i=1，2，3，则P(ξ=2)等于(    )

A.       B.         C.      D.

解析：由P(ξ=1)+P(ξ=2)+P(ξ=3)=1知=1，所以a=3。

于是P(ξ=2)=。

答案：C

5.已知随机变量ξ~B(6，)，则D(2ξ+4)等于(    )

A.6          B.4         C.3         D.9

解析：D(2ξ+4)=4Dξ=4·6··=6。

答案：A

6.已知n个数据x₁，x₂，…，x_n，那么［(x₁－)²+(x₂－)²+…+(x_n－)²］是(    )

A.S²          B.S         C.S^*           D.S^*2

解析：∵S²=［(x₁－)²+(x₂－)²+…+(x_n－)²］。

S^*2=［(x₁－)²+(x₂－)²+…+(x_n－)²］。

故本题应选D。

答案：D

7.对于样本频率分布直方图与总体密度曲线的关系，下列说法中正确的是 (    )

A.频率分布直方图与总体密度曲线无关

B.频率分布直方图就是总体密度曲线

C.样本容量很大的频率分布直方图就是总体密度曲线

D.如果样本容量无限增大，分组的组距无限减小，那么频率分布直方图就会无限接近于总体密度曲线

解析：通过直观图象体会，本题应选D。

答案：D

8.某频率的分布表如下：

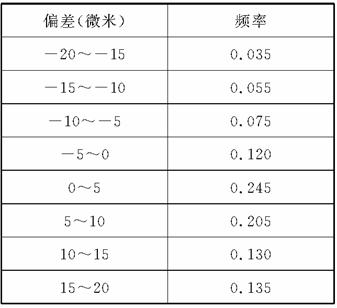
则偏差小于10的累积频率是 (    )

A.0.265        B.0.205     C.0.450          D.0.735

解析：偏差小于10的累积频率应为：0.035+0.055+0.075+0.120+0.245+0.205=0.735。

答案：D

9.一组观察值为4，3，5，6出现的次数分别为3，2，4，2则样本平均值为(    )

A.4.56         B.4.5          C.12.5         D.1.64

解析：样本平均值应为≈4.56。

答案：A

10.某种产品的广告费支出x与销售额y(单位：百万元)之间有如下对应数据

则回归直线方程为(    )

A.=6.5x+17.5         B.=17.5x+6.5

C.=－6.5x+17.5       D.=－17.5x+6.5

解析：，

∴。

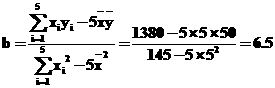a=－b=50－6.5×5=17.5

∴=6.5x+17.5。

答案：A

11.设随机变量ξ的分布列为

P(ξ=k)=，k=0，1，2，…，λ>0是常数，且P(ξ=2)=P(ξ=3)，则P(ξ=4)等于(    )

A.e³                 B.e^－3

C.e^－3                 D.以上答案都不对

解析：由P(ξ=2)=P(ξ=3)，知，，

∵λ²e^－λ≠0，∴λ=3，∴P(ξ=4)=。

答案：B

12.设ξ的概率分布如下，则p等于 (    )

A.           B.          C.          D.

解析：由p₁+p₂+p₃+p₄=1，可知+p++=1，∴p=。

答案：D

二、填空题(每小题4分，计16分)

13.已知随机变量ξ的分布列为

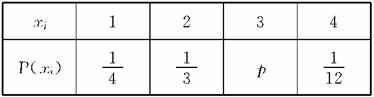
则p=_____，P(1<ξ≤4)=_____。

答案： 

14.已知随机变量ξ~B(n，p)，则Eξ=_____，Dξ=_____。

答案：np  np(1－p)  

15.P(ξ=n)=(n≥2的自然数)      (是/不是)随机变量ξ的一种概率分布。

解析：由P(ξ=n)= ≥0

n=2，3…

又.

故P(ξ=n)=(n≥2)是随机变量ξ的概率分布。

答案：是

16.下面为一组数据观测值的分布情况，估计数值小于a_k的概率为     频率分布表：

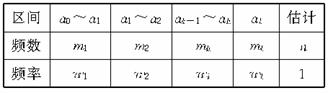
解析：因为数值小于a_k的累积频率为

w₁+w₂+…+w_k=，

所以数值小于a_k的估计概率为。

答案：  

三、解答题

17.(本题12分)某批零件直径服从正态分布N(0.8，0.0004)，(单位：cm).那么，其中直径小于0.79 cm的零件约占多少？

解：μ=0.8，σ=0.02

=(－0.5)=1－(0.5)=1－0.6915=0.3085，即其中直径小于0.79 cm的零件约占30.85%。

18.(12分)设随机变量ξ的概率分布为：

求随机变量η=sin(ξ)的分布列。

解：因为sin()=

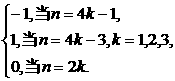
所以，函数η=sin(ξ)的可能值为－1，0，1，而取得这些值的概率分别是：

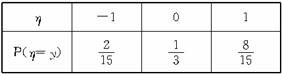
P(η=－1)=.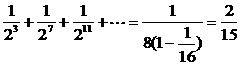

P(η=0)=.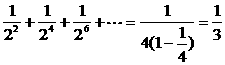

P(η=1)=.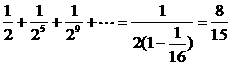

于是得到η的概率分布为：

19.(12分)设随机变量ξ具有分布：P(ξ=k)=，k=1，2，3…求Eξ、Dξ，及σξ。

解：Eξ=·P(ξ=k)= ·+2·+3·+…

+…

二式相减

，

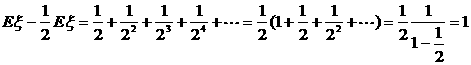∴Eξ=2。

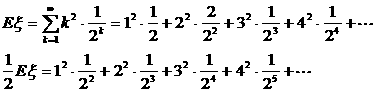
二式相减Eξ²－

乘

上面最后二式相减

，

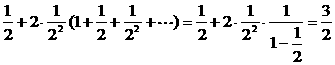∴Eξ ²=6，∴Dξ=Eξ ²－(Eξ)²=6－4=2，∴σξ=。

20.(12分)从某食品厂生产的罐头中，抽查100个罐头的净重，得到如下数，完成表格并画出频率分布直方图。

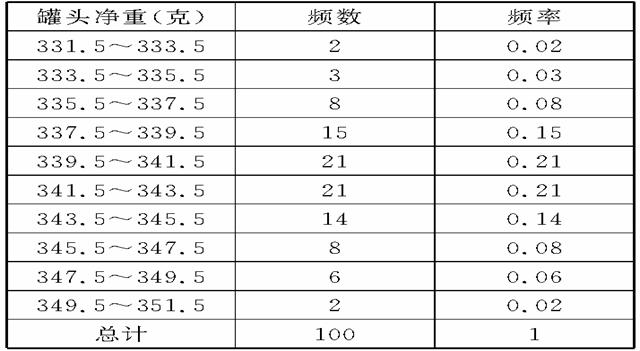
解：

频率分布直方图

21.(12分)对甲、乙的学习成绩进行抽样分析，各抽5门功课.得到的观测值如下：

甲  60  80  70  90  70

乙  80  60  70  80  75

问：甲乙谁的平均成绩好？谁的各门功课发展较平衡。

解：(60+80+70+90+70)=74  (80+60+70+80+75)=73

(14²+6²+4²+16²+4²)=104 

(7²+13²+3²+7²+2²)=56

因为。

所以甲的平均成绩较好，乙的各门发展较平衡。

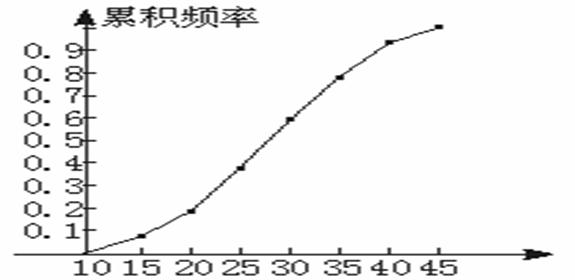
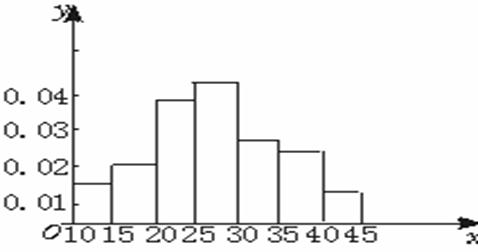
22.(14分)有一容量为50的样本，数据的分组，及各组的频率数如下：

［10，154   ［15，205    ［20，2510   ［25，3011

［30，359   ［35，408    ［40，45)3

(1)列出样本的频率分布表(含累积频率)

(2)画频率分布直方图和累积频率的分布图。

解：频率分布表如下：

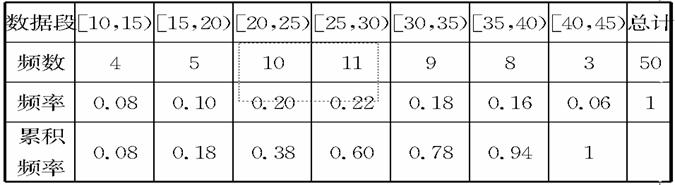
频率分布直方图如图

累积频率分布图如图