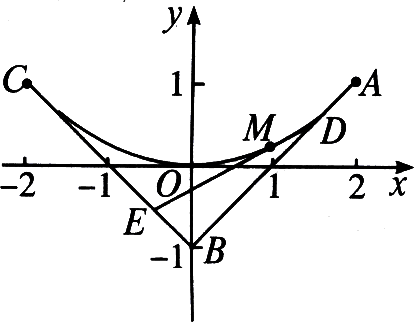网络结构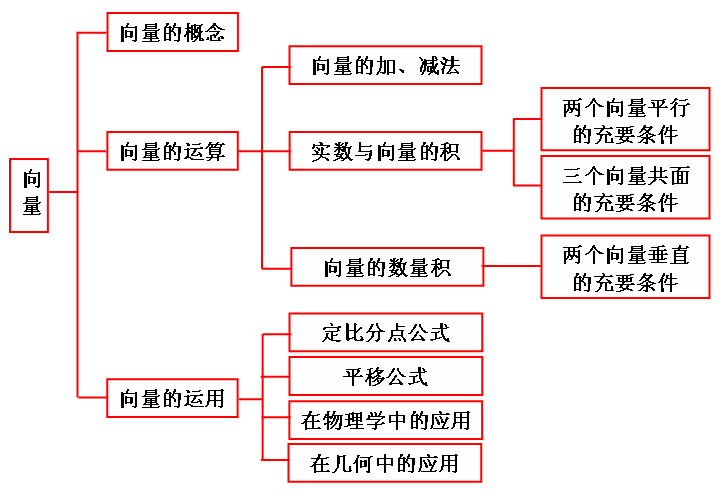
|
|
要点归纳 一、向量的基本知识 1.向量的概念 向量是区别于数量的一种量,它由大小和方向两个因素确定,向量有三种表示法:一是用有向线段来表示;二是用字母`vec(a)`或`vec(AB)`来表示;三是用坐标`vec(a)`=(x,y)来表示.注意共线向量(也称平行向量,方向相同或相反的向量)与相等向量(方向相同且模相等)的联系与区别. 2.向量的运算 向量的运算有加法、减法、数乘向量和向量的数量积四种.注意前三种向量运算的几何表示和四种运算的坐标表示、运算律. 3.向量的定理及相关性质 (1)两个非零向量平行的充要条件 `vec(a)∥vec(b) hArr vec(a)=lambda vec(b)(lambda∈R)`, 设`vec(a)=(x_1,y_1),vec(b)=(x_2,y_2)`, 则`vec(a)∥vec(b) hArr x_1y_2-x_2y_1=0`. (2)两个非零向量垂直的充要条件 `vec(a)_|_vec(b) hArr vec(a)·vec(b)=0`. 设`vec(a)=(x_1,y_1),vec(b)=(x_2,y_2)`,则`vec(a)_|_vec(b) hArr x_1x_2+y_1y_2=0`. (3)向量基本定理 ①平面向量的基本定理:如果有`vec(e_1),vec(e_2)`是同一平面内的两个不共线向量,那么对于这一平面内的任一向量`vec(a)`,有且只有一对实数`lambda_1、lambda_2`使`vec(a)=lambda_1vec(e_1)+lambda_2vec(e_2)`. ②空间向量的基本定理:如果三个向量`vec(a)、vec(b)、vec(c)`不共面,那么对空间任一向量`vec(p)`,存在一个唯一的有序实数组x、y、z,使`vec(p)=x vec(a)+y vec(b)+z vec(c)`. (4)共线与共面定理 ①三点共线定理:平面上三点A、B、C共线的充要条件是:存在实数`alpha、beta`,使`vec(OA)=alpha vec(OB)+beta vec(OC)`,其中`alpha+beta`=1,O为平面内的任一点. ②空间中有四个点P、A、B、C共面的充要条件是:存在实数x、y、x,使`vec(OP)=xvec(OA)+y vec(OB)+Z vec(OC)`,其中x+y+x=1,O为空间中任一点. 4.常用公式及结论 (1)向量模的公式 设`vec(A)`=(x,y,x),则`|vec(A)|=sqrt(x^2+y^2+x^2)`. (2)两点问的距离公式 |vec(P_1P_2)|=sqrt((x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2), 其中`P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2)`. (3)线段的定比分点坐标公式 `{(x=(x_1+lambda x_2)/(1+lambda)),(y=(y_1+lambda y_2)/(1+lambda),(z=(z_1+lambda z_2)/(1+lambda)):}` 其中`P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2),P(x,y,x),vec(P_1P)=lambda vec(PP_2)`. (4)中点坐标公式 `{(x_0=(x_1+x_2)/2),(y_0=(y_1+y_2)/2),(z_0=(z_1+z_2)/2):}`,或`vec(OM)=1/2(vec(OA)+vec(OB))`, M(x_0,y_0,x_0)是线段AB的中点, 其中`A(x_1,y_1,z_1),B(x_2,y_2,z_2)`. (5)两向量的夹角公式 `cos theta=(vec(a)•vec(b))/(|vec(a)||vec(b)|)=(x_1x_2+y_1y_2+z_1z_2)/(sqrt(x_1^2+y_1^2+z_1^2)•sqrt(x_2^2+y_2^2+z_2^2))` 其中0°≤`theta`≤180°,`vec(a)=(x_1,y_1,z_1),vec(b)=(x_2,y_2,z_2)`. (6)图形平移公式 若点P(x,y)按向量`vec(a)=(h,k)`平移至`P'(x',y')`,则 `{(x'=x+h),(y'=y+k):}`. (7)有关向量模的常用结论 ①`|vec(a)|^2=vec(a)•vec(a)=vec(a)^2` , ②`|vec(a)±vec(b)|^2=(vec(a)±vec(b))^2=|vec(a)|^2±2 vec(a)•vec(b)+|vec(b)|^2`; ③`|vec(a)•vec(b)|≤|vec(a)|•|vec(b)|,||vec(a)|-|vec(b)||≤|vec(a)±vec(b)|≤|vec(a)|+|vec(b)|`. 二、向量学科内综合运用 1.平面向量与函数、不等式、三角函数、数列的综合运用当平面向量给出的形式中含有未知数时,由向量平行或 垂直的充要条件可以得到关于该未知数的关系式.在此基础上,可以设计出有关函数、不等式、三角函数、数列的综合问题.此类题的解题思路是转化为代数运算,其转化途径主要有两种: (1)利用向量平行或垂直的充要条件; (2)利用向量数量积的公式和性质. 2.平面向量与解析几何的综合运用 由于向量既能体现“形"的直观位置特征,又具有“数"的良好运算性质,是数形结合与转换的桥梁和纽带.而解析几何也具有数形结合与转换的特征,所以在向量与解析几何知识的交汇处设计试题,已逐渐成为高考命题的一个新的亮点. 平面向量与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,解决此类问题的基本思路是将几何问题坐标化、符号化、数量化,从而将推理转化为运算;或者考虑向量运算的几何意义,利用其几何意义解决有关问题.主要包括以下三种题型: (1)运用向量共线的充要条件处理解析几何中有关平行、共线等问题; (2)运用向量的数量积处理解析几何中有关长度、角度、垂直等问题; (3)运用平面向量综合知识,探求动点轨迹方程,还可再进一步探求曲线的性质. 3.空间向量和立体几何知识的整合 用向量知识解证立体几何问题,常常比用几何法简便,其优点在于:向量可以使立体几何问题代数化,简单的代数运算取代了复杂的几何证明,解题的方向明确,可避免作辅助线及运算繁多的定理、公理等进行推理的思维过程.在立体几何中求空间角、空间距离及处理垂直关系显得尤为方便. |
| 典型案例 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高)
1、已知向量`vec(a)=(sin
theta,1),vec(b)=(1,cos theta),-pi/2<theta<pi/2`.
2、 设函数`f(x)=vec(a)•vec(b)`,其中向量`vec(a)=(2 cosx,1),vec(b)=(cosx,sqrt(3)sin2x),x∈R`. (1)若`f(x)=1-sqrt(3),且x∈[-pi/3,pi/3]`,求x; (2)若函数y=2sin2x的图象按向量`vec(c)(m,n)(|m|<pi/2)`平移后得到函数y=f(x)的图象,求实数m、n的值.
3、 已知`vec(i)、vec(j)`是x、y轴正方向的单位向量,设`vec(a)=(x-sqrt(3))vec(i)+yvec(j),vec(b)=(x+sqrt(3))vec(i)+yvec(j)`,且满足`|vec(a)|+|vec(j)|=4`. (1)求点P(x,y)的轨迹C的方程; (2)如果过点Q(0,m)且方向向量为`vec(c)=(1,1)`的直线`l`与点P的轨迹交于A、B两点,当△AOB的面积取到最大值时,求m的值.
4、 如图,三定点A(2,1),B(0,-1),C(-2,1);三动点D、E、M满足`vec(AD)=tvec(AB)`,`vec(BE)=tvec(BC)`,`vec(DM)=tvec(DE)`,t∈[0,1]. (1)求动直线DE斜率的变化范围; (2)求动点M的轨迹方程. 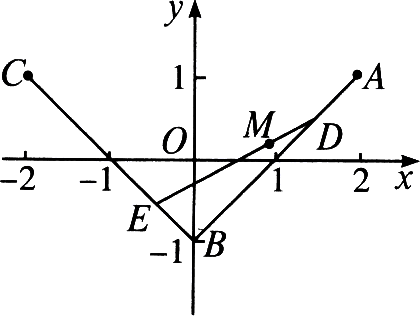
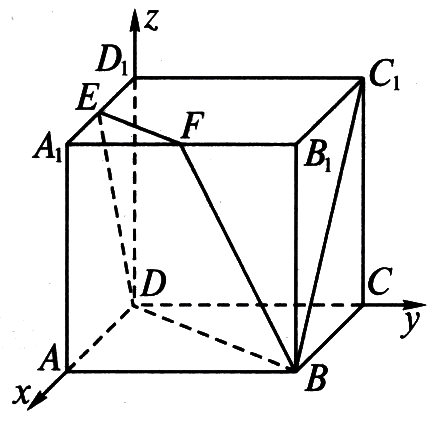
5、 如图,在棱长为2的正方体`ABCD—A_1B_1C_1D_1`中,E、F分别是棱`A_1D_1、A_1B_1`的中点. (1)求异面直线DE与FC。所成的角; (2)求`BC_1`和面`EFBD`所成的角; (3)求`B_1`到面`EFBD`的距离. 
|
|
|
思想感悟 1、用集合的概念解题; |