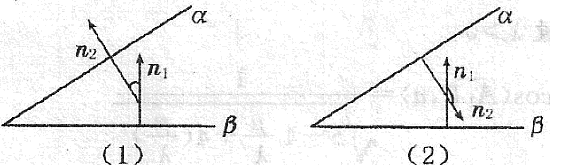|
考纲展示 1、掌握平面的基本性质,会用斜二测画法画水平放置的平面图形的直观图; 能够画出空间两条直线、直线和平面的各种位置关系的图形; 能够根据图形想象它们的位置关系.
2、掌握直线和平面平行的判定定理和性质定理; 理解直线和平面垂直的概念; 掌握直线和平面垂直的判定定理; 掌握三垂线定理及其逆定理.
3、理解空间向量的概念; 掌握空间向量的加法、减法和数乘.
4、了解空间向量的基本定理; 理解空间向量坐标的概念; 掌握空间向量的坐标运算.
5、掌握空间向量的数量积的定义及其性质; 掌握用直角坐标计算空间向量数量积的公式; 掌握空间两点间的距离公式.
6、理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.
7、掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念; 对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离; 掌握直线和平面垂直的性质定理; 掌握两个平面平行、垂直的判定定理和性质定理.
8、了解多面体、凸多面体的概念;了解正多面体的概念.
9、了解棱柱的概念;掌握棱柱的性质,会画直棱柱的直观图.
10、了解棱锥的概念;掌握正棱锥的性质,会画正棱锥的直观图.
11、了解球的概念;掌握球的性质;掌握球的表面积、体积公式. |
|
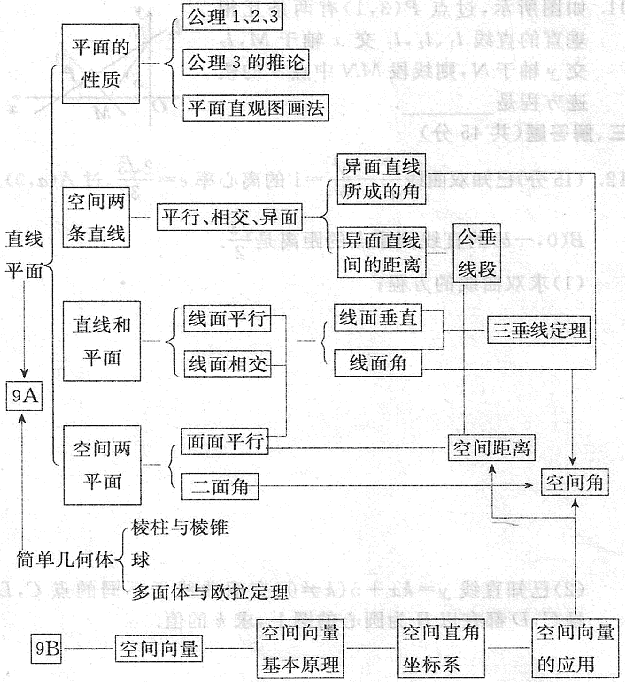
专题结构
|
|
命题特点 1、空间向量的运算 2、利用向量求空间角 3、利用向量求空间距离 |
|
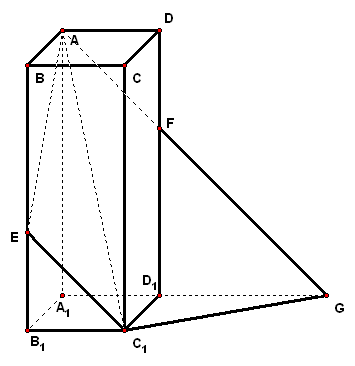
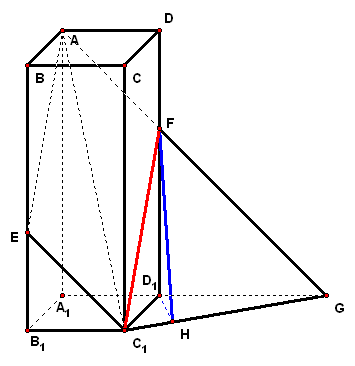
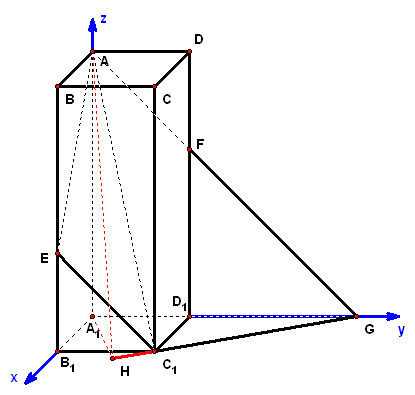
考点案例
(1)设`|vec(c)|=3`,`vec(c)"//"vec(BC)`,求`vec(c)` (2)求`vec(a)`和`vec(b)`的夹角 (3)若`kvec(a)+vec(b)`与`kvec(a)-2vec(b)`互相垂直,求`k`
|
|
|
方法感悟 2、在立体几何中,要证明两线垂直,可选取适当的基底,然后确定各向量的坐标,通过向量数量积的坐标运算结果为`O`来证明,是一个很好的办法.
3、求异面直线所成角的关键是求异面直线上两向量的数量积,而要求两向量的数量积,必须会把所求向量用空间的一组基向量来表示. |