|
考纲展示 1、掌握平面的基本性质,会用斜二测画法画水平放置的平面图形的直观图; 能够画出空间两条直线、直线和平面的各种位置关系的图形; 能够根据图形想象它们的位置关系.
2、掌握直线和平面平行的判定定理和性质定理; 理解直线和平面垂直的概念; 掌握直线和平面垂直的判定定理; 掌握三垂线定理及其逆定理.
3、理解空间向量的概念; 掌握空间向量的加法、减法和数乘.
4、了解空间向量的基本定理; 理解空间向量坐标的概念; 掌握空间向量的坐标运算.
5、掌握空间向量的数量积的定义及其性质; 掌握用直角坐标计算空间向量数量积的公式; 掌握空间两点间的距离公式.
6、理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.
7、掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念; 对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离; 掌握直线和平面垂直的性质定理; 掌握两个平面平行、垂直的判定定理和性质定理.
8、了解多面体、凸多面体的概念;了解正多面体的概念.
9、了解棱柱的概念;掌握棱柱的性质,会画直棱柱的直观图.
10、了解棱锥的概念;掌握正棱锥的性质,会画正棱锥的直观图.
11、了解球的概念;掌握球的性质;掌握球的表面积、体积公式. |
|
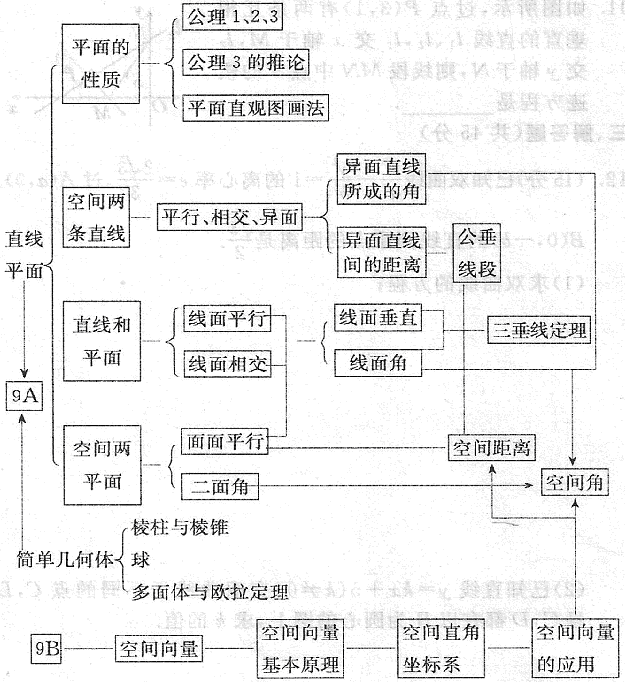
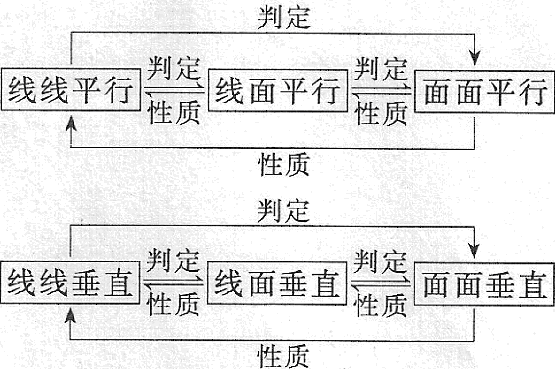
专题结构
|
|
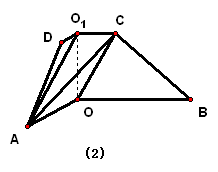
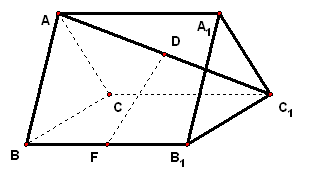
命题特点 1、平面的基本性质 2、平行问题 3、垂直问题 |
|
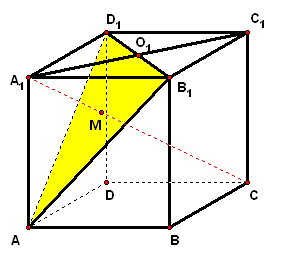
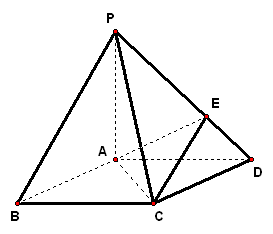
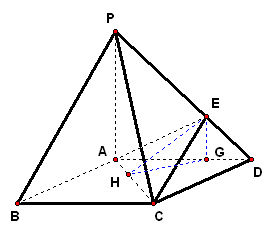
考点案例
|
|
|
方法感悟 1、高考对立体几何的考查突出考查空间想象能力,同时考查逻辑思维能力和演绎推理能力,对空间想像能力有三个方面的要求: (1)根据题设条件想像和画出图形,首先要识别图形,包括几何体的形状、大小,几何体间的位置关系;几何体中各元素在平面上、空间中的相互位置关系以及相对于特定位置的排列顺序; (2)能正确地分析出图形中基本元素及其相互关系; (3)能对图形进行分解、组合与变形. 2、注意立体几何问题向平面几何问题的转化,即立体几何问题平面化;用类比的思想去认识线面的平行与垂直关系,注意垂直与平行之间的联系. 线线、线面、面面的平行与垂直的关系可以通过下列形式转化:
|