第五章平面向量

考纲展示

专题结构

命题特点

考点案例

考能训练

方法感悟

    一、考纲展示
    1、理解向量的概念，掌握向量的几何表示，了解共线向量的概念.
    2、掌握向量的加法和减法.
    3、掌握实数与向量的积，理解两个向量共线的充要条件.
    4、了解平面向量的基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算；
    5、掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的条件.
    6、掌握平面内两点间的距离公式，以及线段的定比分点和中点坐标公式，并且能熟练运用掌握平移公式．

    考点案例
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)
    一、向量的概念与运算
    1、(2006山东烟台5月高三适应性练习)点O在`DeltaABC`内部且满足`vec(OA)+2vec(OB)+2vec(OC)=vec(0)，则DeltaABC`的面积与`DeltaOBC`面积之比为(   )
    A．`5/4`                      B．3                       C．4                  D．5

提示

示范

    二、向量的数量积与运算律
    1、(2006年高考全国卷Ⅱ)已知向量`vec(a)=(sin theta,1),vec(b)=(1,cos theta),-pi/2<theta<pi/2`
    (1)若`vec(a)_|_vec(b)`,求`theta`；
    (2)求`|vec(a)+vec(b)|`的最大值．

提示	示范
无.
解:(1)若`vec(a)_\|_vec(b),则sin theta+cos theta=0`，由此得 `tan theta=-1(-pi/2<theta<pi/2) :. theta=-pi/4` (2)由`vec(a)=(sin theta,1),vec(b)=(1,cos theta)`得 `vec(a)+vec(b)=(sin theta+1,1+cos theta)` `\|vec(a)+vec(b)\|=sqrt((sin theta+1)^2+(1+cos theta)^2)=sqrt(3+2(sin theta+cos theta))=sqrt(3+2sqrt(2)sin(theta+pi/4))` 当`sin(theta+pi/4)=1时，\|vec(a)+vec(b)\|`取得最大值，即当`theta=pi/4`时，`\|vec(a)+vec(b)\|`的最大值为`sqrt(2)+1`．评注: 向量与三角函数结合，题目新颖而又精巧，既符合在知识的“交汇处”构题，又加强了对向量的考查，特别是向量的坐标表示与运算可以大大简化数量积的运算，这类题目涉及的知识有： ① 向量的坐标表示，向量的加法与减法； ② 实数与向量的积，两向量的数量积； ③ 两向量垂直、平行的充要条件； ④ 向量的夹角、向量的长度等．解题时，要理解向量的有关概念，掌握平面向量的坐标运算．向量与三角函数、向量与平面解析几何相结合，在知识交汇点处命题．既是热点，又是重点，一定要加强向量的坐标运算．若`vec(a)=(x_1,y_1),vec(b)=(x_2,y_2),则vec(a)•vec(b)=x_1x_2+y_1y_2`, `cos<vec(a),vec(b)>=(x_1x_2+y_1y_2)/(sqrt(x_1^2+y_1^2)•sqrt(x_2^2+y_2^2))`

   三、距离公式和定比分点
   1、(2006年高考湖北卷)设函数`f(x)=vec(a)•(vec(b)+vec(c)),其中向量vec(a)=(sinx,-cosx),vec(b)=(sinx,-3cosx),vec(c)=(-cosx,sinx),x in RR`
   (1)求函数`f(x)`的最大值和最小正周期；
   (2)将函数`y=f(x)`的图象按向量`vec(d)`平移，使平移后得到的图象关于坐标原点成中心对称，求长度最小的`vec(d)`．

提示	示范
无.
解:(1)由题意得`f(x)=vec(a)•(vec(b)+vec(c))` `= (sinx,-cosx)•(sinx-cosx,sinx-3cosx)` `=sin^2x-2sinxcosx+3cos^2x` `=2+cos2x-sin2x` `=2+sqrt(2)sin(2x+3pi/4)` 故`f(x)`的最大值为`2+sqrt(2)`，最小正周期是`(2pi)/2=pi` (2)由`sin(2x+(3pi)/4)=0得2x+(3pi)/4=kpi,即x=(kpi)/2-(3pi)/8,k in ZZ` 于是`vec(d)=((3pi)/8-(kpi)/2,-2),\|vec(d)\|=sqrt(((3pi)/8-(kpi)/2)^2+4) ,k in ZZ` 因为k为整数，要使`\|vec(d)\|`最小，则只有`k=1,此时vec(d)=(-pi/8,-2)`即为所求．评注:本小题主要考查平面向量数量积的计算方法、三角公式、三角函数的性质及图象的基本知识，考查推理和运算能力．

   四、正、余弦定理，解斜三角形
   1、(2006年高考天津卷)在`DeltaABC中，AC=2，BC=1，cosC=3/4`
   (1)求AB的值；
   (2)求`sin(2A+C)`的值．

提示	示范
无.
解:(1)由余弦定理，`AB^2=AC^2+BC^2-2AC·BCcosC =4+1-2 xx 2 xx 1 xx 3/4=2`，那么，`AB=sqrt(2)` (2)由`cosC=3/4且0<C<pi`，得`sinC=sqrt(1-cos^2(C))=sqrt(7)/4` 由正弦定理，`(AB)/sinC=(BC)/sinA`，解得`sinA=(BCsinC)/AB=sqrt(14)/8`，所以`cosA=(5sqrt(2))/8` 由倍角公式`sin2A=2sinA·cosA=(5sqrt(7))/16`且`cos2A=1-2sin^2A=9/16,` 故`sin(2A+C)=sin2AcosC+cos2AsinC=(3sqrt(7))/8` 评注:以三角形为载体，以三角变换为核心，结合正弦定理和余弦定理综合考查逻辑分析和计算推理能力是高考命题的一个重要方向，因此要特别关注三角函数在解斜三角形中的灵活应用．

考能训练

    一、选择题
    1、(2006山东潍坊市高三统考)若O是`DeltaABC`所在平面内一点，且满足`|vec(OB)-vec(OC)|=|vec(OB)+vec(OC)-2vec(OA)|`，则`DeltaABC`的形状为(   )
    A、直角三角形        B、等腰三角形            C、等腰直角三角形         D、等边三角形
    2、(2006陕西高考，9理)已知非零向量`vec(AB)与vec(AC)`满足`(vec(AB)/| vec(AB)|+vec(AC)/|vec(AC)|)·vec(BC)=0且vec(AB)/| vec(AB)|·vec(AC)/|vec(AC)|=1/2`则`DeltaABC`为(   )
    A、等边三角形         B、直角三角形            C、等腰非等边三角形       D、三边均不相等的三角形
    3、(2004湖北八市调研题)已知`vec(OB)=(2,0),vec(OC)=(2,2),vec(CA)=(sqrt(2)cos alpha, sqrt(2)sin alpha)(a in RR)，则vec(OA)与vec(OB)`夹角的范围为(其中O为坐标原点)(   )
    A、`[0，pi/4]`               B、`[pi/4,(5pi)/12]`             C、`[(5pi)/12,pi/2]`               D、`[pi/12,(5pi)/12]`
    4、(2006山东烟台高三5月适应性训练)已知直线`x+y=a`与圆`x^2+y^2=4`交于A、B两点，且`|vec(OA)+vec(OB)|=| vec(OA)-vec(OB)|`，其中O为原点，则实数a的值为(   )
    A、2                 B、-2                       C、2或-2                 D、`sqrt(6)或sqrt(-6)`
    5、已知`DeltaABC的三个顶点A、B、C及平面内一点P满足vec(PA)+vec(PB)+vec(PC)=vec(AB),则点P与DeltaABC`的关系为(    )
    A、`P在DeltaABC`内部       B、`P在DeltaABC`外部       C、`P在AB`边所在直线上     D、`P是AC`边的一个三等分点
    二、填空题
    6、(2005上海高考，3理)直角坐标平面`xOy中，若定点A(1,2)与动点P(x,y)`满足`vec(OP)·vec(OA)=4`，则点P的轨迹方程是______
    7、(2006北京东城高三综合练习)若`vec(b)=(3,4),|vec(a)-vec(b)|=1，则|vec(a)|`的最大值与最小值的差是______
    三、解答题
    8、已知向量`vec(a)=(3cos alpha,sin alpha), alpha in (0,pi/2),vec(e)=(1,0)，向量vec(a)`与`vec(e)的夹角为beta,求tan(alpha-beta)的最大值，并求相应的alpha`的值．

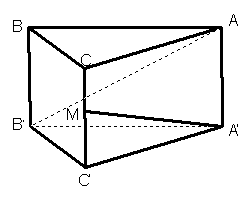
9、如图，已知直三棱柱`ABC-A_1B_1C_1中，/_ACB=90^0,/_BAC=30^0,BC=1,AA_1=sqrt(6)`，`M是C C_1`的中点，求证：`vec(AB_1)_|_vec(A_1M)`．

    10、一非零向量列`{a_n}满足vec(a_1)=(x_1,y_1),vec(a_n)=(x_n,y_n)=1/2(x_n-1-y_(n-1),x_(n-1)+y_(n-1))(n>=2)`
    (1)证明：`{|vec(a_n)|}`是等比数列；
    (2)求`vec(a_(n-1))与vec(a_n)的夹角theta(n>=2),若vec(b_n)=2n theta_n-1,S_n=vec(b_1)+vec(b_2)+…+vec(b_n)，求S_n`；
    (3)设`vec(a_1)=(1,2),把vec(a_1),vec(a_2), …,vec(a_n),…`中所有与`vec(a_1)`共线的向量按照原来的顺序排成一列，记为`vec(b_1),vec(b_2), …,vec(b_n), …，令vec(OB_n)=vec(b_1)+vec(b_2)+vec(b_3)+ …+vec(b_n)(O为坐标原点)`,求点列`{B_n}`的极限点B的坐标(注：若点`B_n`的坐标为`(t_n,s_n)且lim_(n rarr oo)t_n=t,lim_(n rarr oo)s_n=s,则点B(t,s)为点列{B_n}`的极限点)．

参考答案

    一、选择题
    1、(2006山东潍坊市高三统考)若O是`DeltaABC`所在平面内一点，且满足`|vec(OB)-vec(OC)|=|vec(OB)+vec(OC)-2vec(OA)|`，则`DeltaABC`的形状为( A )
    A、直角三角形         B、等腰三角形           C、等腰直角三角形          D、等边三角形
    2、(2006陕西高考，9理)已知非零向量`vec(AB)与vec(AC)`满足`(vec(AB)/| vec(AB)|+vec(AC)/|vec(AC)|)·vec(BC)=0且vec(AB)/| vec(AB)|·vec(AC)/|vec(AC)|=1/2`则`DeltaABC`为( A )
    A、等边三角形         B、直角三角形           C、等腰非等边三角形        D、三边均不相等的三角形
    3、(2004湖北八市调研题)已知`vec(OB)=(2,0),vec(OC)=(2,2),vec(CA)=(sqrt(2)cos alpha, sqrt(2)sin alpha)(a in RR)，则vec(OA)与vec(OB)`夹角的范围为(其中O为坐标原点)( D )
    A、`[0，pi/4]`            B、`[pi/4,(5pi)/12]`           C、`[(5pi)/12,pi/2]`           D、`[pi/12,(5pi)/12]`
    4、(2006山东烟台高三5月适应性训练)已知直线`x+y=a`与圆`x^2+y^2=4`交于A、B两点，且`|vec(OA)+vec(OB)|=| vec(OA)-vec(OB)|`，其中O为原点，则实数a的值为( C )
    A、2                  B、-2                   C、2或-2                   D、`sqrt(6)或sqrt(-6)`
    5、已知`DeltaABC`的三个顶点A、B、C及平面内一点P满足`vec(PA)+vec(PB)+vec(PC)=vec(AB)`,则点P与`DeltaABC`的关系为( D )
    A、`P在DeltaABC`内部      B、`P在DeltaABC`外部     C、`P在AB`边所在直线上      D、`P是AC`边的一个三等分点
    二、填空题
    6、(2005上海高考，3理)直角坐标平面xOy中，若定点A(1,2)与动点P(x,y)满足`vec(OP)·vec(OA)=4`，则点P的轨迹方程是______
    答案:`x+2y-4=0`
    7、(2006北京东城高三综合练习)若`vec(b)=(3,4),|vec(a)-vec(b)|=1，则|vec(a)|`的最大值与最小值的差是______
    答案：2
    三、解答题
    8、已知向量`vec(a)=(3cos alpha,sin alpha), alpha in (0,pi/2),vec(e)=(1,0)`，向量`vec(a)`与`vec(e)的夹角为beta,求tan(alpha-beta)的最大值，并求相应的alpha`的值．

    答案：`alpha=pi/3`时，`tan(alpha-beta)`有最大值`sqrt(3)/3`
    9、如图，已知直三棱柱`ABC-A_1B_1C_1中，/_ACB=90^0,/_BAC=30^0,BC=1,AA_1=sqrt(6)`，`M是CC_1`的中点，求证：`vec(AB_1)_|_vec(A_1M)`．

    证明：因为`vec(AB_1)·vec(A_1M)=(vec(AA_1)+vec(A_1B_1))·(vec(A_1C_1)+vec(C_1M))=vec(AA_1)·vec(A_1C_1)+vec(AA_1)·vec(C_1M)+vec(A_1B_1)·vec(A_1C_1)+vec(A_1B_1)·vec(C_1M)`,
    由向量`vec(AA_1)_|_vec(A_1C_1),vec(AA_1)"//"vec(C_1M)`且方向相反，
    `vec(A_1B_1)_|_vec(C_1M) rArr vec(AA_1)·vec(A_1C_1)=0`
    `vec(AA_1)·vec(C_1M)=|vec(AA_1)||vec(C_1M)|cos180^0=sqrt(6) xx sqrt(6)/2 xx (-1)=-3`
    `vec(A_1B_1)·vec(C_1M)=0`
    又由`/_BAC=30^0,/_ACB=90^0,BC=1 rArr vec(A_1B_1)·vec(A_1C_1)=|vec(A_1B_1)||vec(A_1C_1)|cos30^0=2 xx sqrt(3) xx sqrt(3)/2=3`
    所以`vec(AB_1)vec(A_1M)=0-3+3+0=0`
    所以`vec(AB_1)_|_vec(A_1M)`
    10、一非零向量列`{a_n}满足vec(a_1)=(x_1,y_1),vec(a_n)=(x_n,y_n)=1/2(x_n-1-y_(n-1),x_(n-1)+y_(n-1))(n>=2)`
    (1)证明：`{|vec(a_n)|}`是等比数列；
    (2)求`vec(a_(n-1))与vec(a_n)的夹角theta(n>=2),若vec(b_n)=2n theta_n,S_n=vec(b_1)+vec(b_2)+…+vec(b_n)，求S_n`；
    (3)设`vec(a_1)=(1,2),把vec(a_1),vec(a_2), …,vec(a_n),…`中所有与`vec(a_1)`共线的向量按照原来的顺序排成一列，记为`vec(b_1),vec(b_2), …,vec(b_n)`, …，令`vec(OB_n)=vec(b_1)+vec(b_2)+vec(b_3)+ …+vec(b_n)`(O为坐标原点),求点列`{B_n}`的极限点B的坐标(注：若点`B_n`的坐标为`(t_n,s_n)且lim_(n rarr oo)t_n=t,lim_(n rarr oo)s_n=s,则点B(t,s)为点列{B_n}`的极限点)．
    答案：(1)`|a_n|=1/2sqrt((x_(n-1)-y_(n-1))^2+(x_(n-1)+y_(n-1))^2)=sqrt(2)/2sqrt(x_(n-1)^2+y_(n-1)^2)=sqrt(2)/2|a_(n-1)|`对任意`n>=2`恒成立，即`|a_n|=sqrt(2)/2|a_(n-1)|`，故`{|a_(n-1)|}`是首项为`{a_1}`，公比为`sqrt(2)/2`的等比数列；
    (2)`S_n=pi/4(n^2+n)-n`
    (3)`B(4/5,8/5)`

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。