|
应用训练 |
1、命题p:x=`pi`是y=|sinx|的一条对称轴;q:2`pi`是y=|sinx|的最小正周期.下列复合命题:①p或q;②p且q;
③非p;④非q.其中真命题有( )
A.O个 B.1个 C.2个 D.3个
2、已知函数`y=e^x`的图象与函数y=f(x)的图象关于直线y=x对称,则( )
A.`f(2x)=e^(2x)(x∈R)`
B.`f(2x)=ln2•lnx(x>O)`
C.`f(2x)=2e^(2x)(x∈R)`
D.`f(2x)=lnx+ln2(x>O)`
3、已知数列`{a_n}`的通项公式`a_n=(2/3)^(n-1)[(2/3)^(n-1)-1]`,则下列表达正确的是(
)
A.最大项为`a_1`,最小项为`a_3`
B.最大项为`a_1`,最小项不存在
C.最大项不存在,最小项为`a_3`
D.最大项为`a_1`,最小项为`a_4`
4、某邮局只有0.60元、0.80元、1.10元的三种邮票.现有邮资为7.50元的邮件一件,为使粘贴邮票的张数最少,且资费恰为7.50元,则最少要购买邮票(
)
A.7张 B.8张 C.9张 D.10张
5、设向量`vec(a)=(1,-3),vec(b)=(-2,4),vec(c)=(-1,-2)`,若表示向量`4vec(a)`、`4vec(b)-2vec(c)`、`2(vec(a)-vec(c))`、`vec(d)`的有向线
段首尾相接能构成四边形,则向量`vec(d)`为( )
A.(2,6) B.(-2,6) C.(2,-6) D.(-2,-6)
6、(原11)命题A:底面为正三角形,且顶点在底面的射影为底面中
心的三棱锥是正三棱锥.命题A的等价命题B可以是:
底面为正三角形,且______的三棱锥是正三棱锥.
7、(原13)给出如下三个函数:
①`f(x)=(x-1)^3`;②`f(x)=k(x-1)`;③`f(x)={(1,x>1),(0,x=1),(-2,x<1):}`
则同时满足性质:(1)对于任意的`x_1、x_2∈R(x_1≠x_2)`,有`(f(x_2)-f(x_1))/(x_2-x_1)>0`;(2)图象关于点(1,0)成
中心对称图形的函数序号为____.
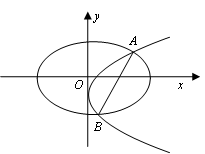
8、(原13)已知椭圆`C_1:x^2/4+y^2/3=1`,抛物线`C_2:(y-m)^2=2px(p>0)`,且`C_1、C_2`的公共弦AB过椭
圆`C_1`的右焦点.
(1)当AB⊥x轴时,求m、p的值,并判断抛物线`C_2`的焦
点是否在直线AB上;
(2)是否存在m、p的值,使抛物线`C_2`的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说
明理由.
|
|
参考答案 |
1、命题p:x=`pi`是y=|sinx|的一条对称轴;q:2`pi`是y=|sinx|的最小正周期.下列复合命题:①p或q;②p且q;
③非p;④非q.其中真命题有( C )
A.O个 B.1个 C.2个 D.3个
2、已知函数`y=e^x`的图象与函数y=f(x)的图象关于直线y=x对称,则(
D )
A.`f(2x)=e^(2x)(x∈R)`
B.`f(2x)=ln2•lnx(x>O)`
C.`f(2x)=2e^(2x)(x∈R)`
D.`f(2x)=lnx+ln2(x>O)`
3、已知数列`{a_n}`的通项公式`a_n=(2/3)^(n-1)[(2/3)^(n-1)-1]`,则下列表达正确的是(
A )
A.最大项为`a_1`,最小项为`a_3`
B.最大项为`a_1`,最小项不存在
C.最大项不存在,最小项为`a_3`
D.最大项为`a_1`,最小项为`a_4`
4、某邮局只有0.60元、0.80元、1.10元的三种邮票.现有邮资为7.50元的邮件一件,为使粘贴邮票的张数最少,且资费恰为7.50元,则最少要购买邮票(
B
)
A.7张 B.8张 C.9张 D.10张
5、设向量`vec(a)=(1,-3),vec(b)=(-2,4),vec(c)=(-1,-2)`,若表示向量`4vec(a)`、`4vec(b)-2vec(c)`、`2(vec(a)-vec(c))`、`vec(d)`的有向线
段首尾相接能构成四边形,则向量`vec(d)`为( D )
A.(2,6) B.(-2,6) C.(2,-6) D.(-2,-6)
6、命题A:底面为正三角形,且顶点在底面的射影为底面中
心的三棱锥是正三棱锥.命题A的等价命题B可以是:
底面为正三角形,且______的三棱锥是正三棱锥.
答案:侧棱相等(或侧棱与底面所成角相等……)
7、给出如下三个函数:
①`f(x)=(x-1)^3`;②`f(x)=k(x-1)`;③`f(x)={(1,x>1),(0,x=1),(-2,x<1):}`
则同时满足性质:(1)对于任意的`x_1、x_2∈R(x_1≠x_2)`,有`(f(x_2)-f(x_1))/(x_2-x_1)>0`;(2)图象关于点(1,0)成
中心对称图形的函数序号为____.
答案:①
8、(原14)已知椭圆`C_1:x^2/4+y^2/3=1`,抛物线`C_2:(y-m)^2=2px(p>0)`,且`C_1、C_2`的公共弦AB过椭
圆`C_1`的右焦点.
(1)当AB⊥x轴时,求m、p的值,并判断抛物线`C_2`的焦点是否在直线AB上;
(2)是否存在m、p的值,使抛物线`C_2`的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说
明理由.
答案:
解:(I)当AB⊥x轴时,点A、B关于x轴对称,
所以m=0,直线AB的方程为:x =1,
从而点A的坐标为`(1,3/2)`或`(1,-3/2)`.
因为点A在抛物线上.所以`9/4=2p`,
即`p=9/8`.此时C2的焦点坐标为(`9/16`,0),该焦点不在直线AB上.
(II)解法一: 假设存在m、p的值使C2的焦点恰在直线AB上,
由(I)知直线AB的斜率存在,故可设直线AB的方程为`y=k(x-1)`.
由`{(y=k(x-1)),(x^2/4+y^2/3=1):}`消去y得`(3+4k^2)x^2-8k^2x+4k^2-12=0`…………①
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=(8k^2)/(3+4k^2).
由{((y-m)^2=2px),(y=k(x-1):}
消去y得`(kx-k-m)^2=2px `. ………………②
因为C2的焦点`F`(p/2,m)`在直线`y=k(x-1)`上,
所以`m=k(p/2-1)`,即`m+k=(kp)/2`.代入②有`(kx-(kp)/2)^2=2px`.
即`k^2x^2-p(k^2+2)x+(k^2p^2)/4=0`. …………………③
由于x1,x2也是方程③的两根,所以x1+x2=`(p(k^2+2))/(k^2)`.
从而`(8k^2)/(3+4k^2)=(p(k^2+2))/( k^2)`.
解得`p=(8k^2)/((4k^2+3)(k^2+2))`……………④
又AB过`C_1、C_2`的焦点,所以
`|AB|=(x_1+p/2)+(x_2+p/2)=x_1+x_2+p=(2-1/2x_1)+( 2-1/2x_2)`,
则`p=4-3/2(x_1+x_2)=4-(12k^2)/(4k^2+3)=
(4k^2+12)/(4k^2+3)`…………………………⑤
由④、⑤式得`(8k^2)/((4k^2+3)(k^2+2))=
(4k^2+12)/(4k^2+3)`,即`k^4-5k^2-6=0`.
解得`k^2=6`于是`k=+-sqrt(6),p=4/3`
因为C2的焦点`F’(2/3,m)`在直线`y=+-sqrt(6)(x-1)`上,所以`m=+-sqrt(6)(2/3-1)`.
∴`m=sqrt(6)/3`或`m=-sqrt(6)/3`.
由上知,满足条件的m、p存在,且`m=sqrt(6)/3`或`m=-sqrt(6)/3`,`p=4/3`.
解法二: 设A、B的坐标分别为`(x_1,y_1) ,( x_2,y_2)`.
因为AB既过C1的右焦点F(1,0),又过C2的焦点`F’(p/2,m)`,
所以`|AB|=(x_1+p/2)+(x_2+p/2)=x_1+x_2+p=(2-1/2x_1)+( 2-1/2x_2)`.
即` x_1+x_2=2/3(4-p)`. ……①
由(Ⅰ)知` x_1≠x_2,p≠2`,
于是直线AB的斜率`k=( y_2-y_1)/( x_2-x_1)=(m-0)/(p/2-1)=(2m)/(p-2)`, ……②
且直线AB的方程是`y=(2m)/(p-2)(x-1)`,
所以`y_1+y_2=(2m)/(p-2)(x_1+x_2-2)=(4m(1-p))/(3(p-2))`. ……③
又因为`{(3x_1^2+4y_1^2=12),( 3x_2^2+4y_2^2=12):}`,所以
`3(x_1+x_2)+4(y_1+y_2)*( y_2-y_1)/( x_2-x_1)=0`. ……④
将①、②、③代入④得`m^2=(3(p-4)(p-2)^2)/(16(1-p))`. ……………⑤
因为`{((y_1-m)^2=2px_1),( (y_2-m)^2=2px_2):}`,所以
` y_1+y_2-2m=2p( x_2-x_1) / ( y_2-y_1) `. …………⑥
将②、③代入⑥得`m^2=(3p(p-2)^2)/(16-10p)` ……………⑦
由⑤、⑦得`(3(p-4)(p-2)^2)/(16(1-p))
=(3p(p-2)^2)/(16-10p)`即`3p^2+20p-32=0`
解得`p=4/3`或`p=-8(舍去)`.将`p=4/3`代入⑤得`m^2=2/3`,
∴`m=sqrt(6)/3`或`m=-sqrt(6)/3`.
由上知,满足条件的m、p存在,且`m=sqrt(6)/3`或`m=-sqrt(6)/3`,`p=4/3`.
|
|
|