|
一、复习目标 二、重点难点 三、特别提示 |
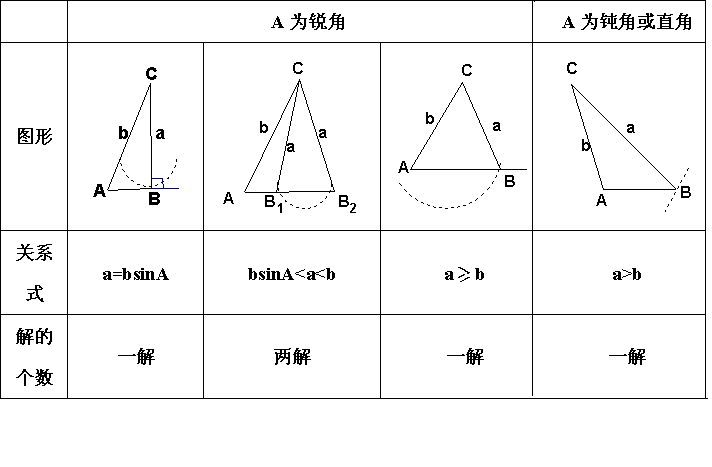
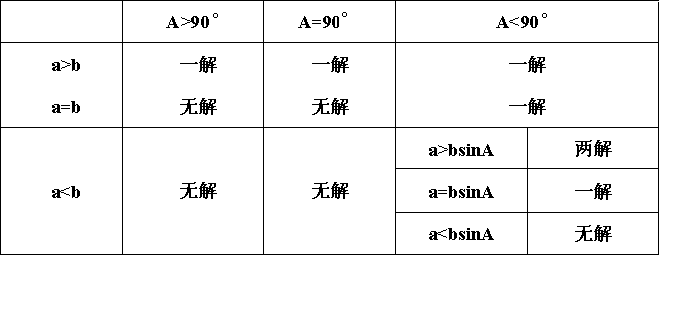
| 知识梳理 1、正弦定理 `a/sinA=b/sinB=c/sinC=2R`,其中`R`是`DeltaABC`的外接圆半径. 2、余弦定理 `a^2=b^2+c^2-2bc cosA,b^2=c^2+a^2-2ac cosB,c^2=a^2+b^2-2ab cosC`, `cosA=(b^2+c^2-a^2)/(2bc),cosB=(a^2+c^2-b^2)/(2ac),cosC=(a^2+b^2-c^2)/(2ab)` 余弦定理的有关问题: (2)在`DeltaABC`中,若`a^2<b^2+c^2`,则______,反之成立. 在`DeltaABC`中,若`a^2=b^2+c^2`,则______,反之成立. 在`DeltaABC`中,若`a^2>b^2+c^2`,则______,反之成立. 3、三角形中的常见结论 (1)`A+B+C=180°`. (2)在三角形中大边对大角,反之亦然. (3)在任意两边之和大于第三边,任意两边之差小于第三边. 4、解斜三角形的类型 解斜三角形有下表所示的四种情况:
|
|
应用举例
二、案例示范 1、在`DeltaABC`中,已知`a=sqrt3,b=sqrt2,B=45°`,求边`c`.
2、如图,在`DeltaABC`中,`AC=2,BC=1,cosC=3/4`.
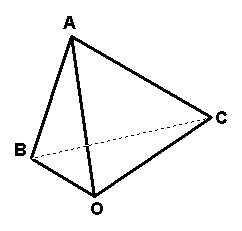
3、如图,海岛O上有一座海拔1000m高的山,山顶上设有一个观察站A.上午11时测得一轮船在岛北偏东`60°`的C处,俯角为`30°`;11时30分又测得该船在岛的北偏西`60°`的B处,俯角为`60°`.求该船的航行速度.
|
|
实践体验
1、在`DeltaABC`中,`a、b、c`分别为角`A、B、C`的对边,`S`为`DeltaABC`的面积,且`4sinBsin^2(pi/4+B/2)+cos2B=1+sqrt(3)`
|
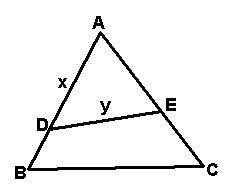
| 拓展探究 在`DeltaABC`中,已知`(a^2+b^2)sin(A-B)=(a^2-b^2)·sin(A+B)`,试判断该三角形的形状.
|
|
|
|
|
学习感悟 |