|
一、复习目标 二、重点难点 三、特别提示 |
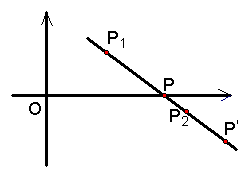
| 知识梳理 1、线段的定比分点 (2)线段定比分点坐标公式 特别地,当`P`是`vec(P_1P_2)`的中点时,有`{(x=(x_1+x_2)/2),(y=(y_1+y_2)/2):}`,这是中点坐标公式. 2、图形的平移 (1)平移 (2)平移公式 (3)函数图象的平移,实质是点的平移问题,可由平移公式化简方程. |
|
应用举例
二、案例示范 1、线段AB的端点坐标分别为`A(-1,1)`,`B(-2,0)`且`|AC|=sqrt2|CB|`,当`A`、`B`、`C`三点共线时,求`C`点的坐标.
2、设函数`f(x)=vec(a)·(vec(b)+vec(c))`,其中向量`vec(a)=(sinx,-cosx),vec(b)=(sinx,-3cosx),vec(c)=(-cosx,sinx),x in RR` (1)求函数`f(x)` 的最大值和最小正周期; (2)将函数`f(x)`的图象按向量`vec(d)`平移,使平移后得到的图象关于坐标原点成中心对称,求长度最小的`vec(d)`.
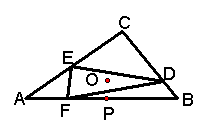
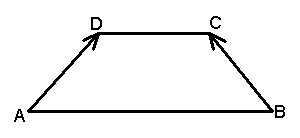
3、(1)在`DeltaABC`中,`D`是`BC`上一点,`vec(BD)/vec(DC)=1/2`,设`vec(AB)=vec(a)`,`vec(AC)=vec(b)`,试用`vec(a)`,`vec(b)`表示`vec(AD)`; (2)设`D`、`E`、`F`分别三等分`DeltaABC`的所在各边即`BC=3BD`,`CA=3CE`,`AB=3AF`(如下图)
|
|
实践体验
1、设曲线C的方程为`y=x^3-x`,将曲线C按向量`vec(a)=(h,k)`平移后得曲线`C_1`.
2、已知曲线`x^2+2y^2+4x+4y+4=0`按向量`vec(a)=(2,1)`平移后得到曲线`C`. (1)求曲线`C`的方程;
|
| 拓展探究 已知点`A(-1,6)`和`B(3,0)`,在直线`AB`上求一点`P`,使`|vec(AP)|=1/3|vec(AB)|`.
|
|
|
|
|
学习感悟 |