|
一、复习目标 掌握平面向量的数量积及其几何意义;了解用平面向量的数量积处理有关长度、角度和垂直的问题;掌握向量垂直的条件. 二、重点难点 三、特别提示 |
| 知识梳理 1、向量数量积的定义 (1)向量`vec(a)`与`vec(b)`的夹角 当`theta=pi/2`时,`vec(a)`与`vec(b)`垂直,记作`vec(a)_|_vec(b)`; 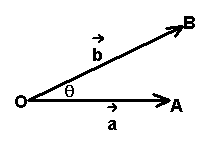 当`theta=0`时,`vec(a)`与`vec(b)`同向;当`theta=pi`时,`vec(a)`与`vec(b)`反向. 当`theta=0`时,`vec(a)`与`vec(b)`同向;当`theta=pi`时,`vec(a)`与`vec(b)`反向.(2)`vec(a)`与`vec(b)`的数量积 2、向量数量积的性质 (1)`vec(e)·vec(a)=vec(a)·vec(e)=|vec(a)|cos theta`. (2)`vec(a)_|_vec(b) hArr vec(a)·vec(b)=0`. (3)当`vec(a)`与`vec(b)`同向时,`vec(a)·vec(b)=|vec(a)||vec(b)|`; 当`vec(a)`与`vec(b)`反向时,`vec(a)·vec(b)=-|vec(a)||vec(b)|`; 特别地,`vec(a)·vec(a)=|vec(a)|^2`或`|vec(a)|=sqrt(vec(a)·vec(a))`. (4)`cos theta =(vec(a)·vec(b))/(|vec(a)||vec(b)|)`. (5)`|vec(a)·vec(b)|<=|vec(a)||vec(b)|` 3、向量数量积的运算律 (1)`vec(a)·vec(b)=vec(b)·vec(a)`(交换律) (2)`(lambda vec(a))·vec(b)=lambda(vec(a)·vec(b))=vec(a)·(lambda vec(b))` (3)`(vec(a)+vec(b))·vec(c)=vec(a)·vec(c)+vec(b)·vec(c)` 4、平面向量数量积的坐标表示 (1)若`vec(a)=(x_1,y_1)`,`vec(b)=(x_2,y_2)`,则`vec(a)·vec(b)=x_1x_2+y_1y_2` (2)设`vec(a)=(x,y)`,则`| vec(a) |=sqrt(x^2+y^2)` |
|
应用举例
二、案例示范 1、已知`vec(a)=(2,3)`,`vec(b)=(-1,-2)`,`vec(c)=(2,1)`,试求`vec(a) (vec(b)·vec(c))`和`(vec(a) ·vec(b)) vec(c)`的值.
2、设向量`vec(a),vec(b),vec(c)`满足` vec(a)+vec(b)+vec(c)=vec(0)`,`(vec(a)-vec(b))_|_vec(c)`,`vec(a)_|_vec(b)`,若`|vec(a)|=1`,则`|vec(a)|^2+|vec(b)|^2+|vec(c)|^2`的值是
3、 已知平面四边形`ABCD`中,`vec(AB)=vec(a),vec(BC)=vec(b),vec(CD)=vec(c),vec(DA)=vec(d)`,且`vec(a)·vec(b)=vec(b)·vec(c)=vec(c)·vec(d)=vec(d)·vec(a)`,试判断四边形`ABCD`的形状.
|
|
实践体验
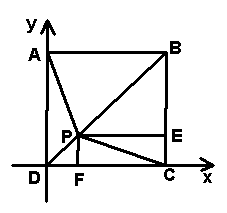
2、如图所示,`P`是正方形`ABCD`的对角线`BD`上一点,`PECF`是矩形,用向量法证明: (1)`PA=EF`; (2)`PA_|_EF`
|
| 拓展探究 已知`|vec(a)|=4,|vec(b)=3|,(2vec(a)-3vec(b))·(2vec(a)+vec(b))=61` (1)求`vec(a)`与`vec(b)`的夹角`theta`; (2)求`|vec(a)+vec(b)|`; (3)若`vec(AB)=a,vec(AC)=vec(b)`,作`DeltaABC`,求`DeltaABC`的面积.
|
|
|
|
|
学习感悟 |