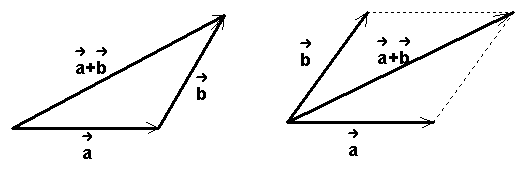|
一、复习目标
|
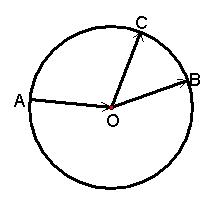
| 知识梳理 1、向量的有关概念 (1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或称模). (2)零向量:长度为`0`的向量叫做零向量,其方向是任意的. (3)单位向量:长度等于1个单位长度的向量. (4)平行向量:方向相同或相反的一组向量.平行向量又叫共线向量,任一组平行向量都可以平移到同一直线上.规定:` vec(0)`与任一向量平行. (5)相等向量:长度相等且方向相同的向量. (6)相反向量:长度相等且方向相反的向量. 2、向量的表示方法 (1) 字母表示法,如:`vec(a)`,`vec(AB)`等. (2) 几何表示法:用一条有向线段表示向量. 3、向量的加法和减法 (1)加法 ①法则:向量加法的三角形法则,向量加法的平行四边形法则.加法定义即三角形法则;以`vec(a)`、`vec(b)`为邻边作平行四边形`ABCD`(取同一起点),即`vec(AB)=vec(a)`,`vec(AD)=vec(b)`,则`vec(AC)`即为`vec(a)`、`vec(b)`的和. ②运算性质: `vec(a)+vec(b)=vec(b)+vec(a)`(交换律) `(vec(a)+vec(b))+vec(c)=vec(a)+(vec(b)+vec(c))`(结合律) `vec(a)+vec(0)=vec(a)=vec(0)+vec(a)` ③加法的几何意义:从法则可以看出,如图所示
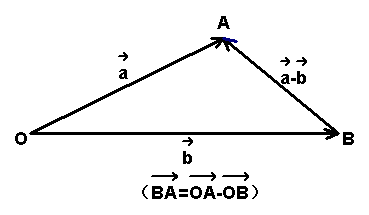
(2)减法
4、实数与向量的积 |
|
应用举例
二、案例示范
1、判断下列命题的真假
A.`pi/6` B.`pi/3` C.`pi/2` D.`(2pi)/3`
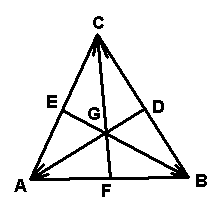
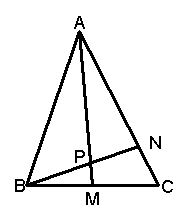
3.如图,设`C`是`△ABC`的重心.求证:`vec(GA)+vec(GB)+vec(GC)=0`.
|
|
实践体验
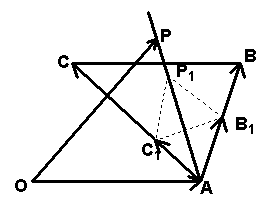
2、`O`是平面上一定点,`A`、`B`、`C`是平面上不共线的三个点,动点`P`满足`vec(OP)=vec(OA)+lambda(vec(AB)/|vec(AB)|+vec(AC)/|vec(AC)|),lambda in [0,+oo)`,则P的轨迹一定通过`DeltaABC`的( ) A.外心 B.内心 C.重心 D.垂心
|
| 拓展探究 设点G是`DeltaABC`所在平面内一点,且`vec(GA)+vec(GB)+vec(GC)=vec(0)`,则点`G`是`DeltaABC`的( ) A.重心 B.内心 C.外心 D.垂心
|
|
|
|
|
学习感悟
1、向量不同于数量.向量既有大小,又有方向.向量的模可以比较大小,但向量不能比较大小. |