三、解答题

20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）

在平面直角坐标系O中，直线与抛物线＝2相交于A、B两点．

（1）求证：“如果直线过点T（3，0），那么＝3”是真命题；

（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．

解：（1）如果直线轴，则

        如果直线与轴不垂直，设直线的方程为，

 ∴

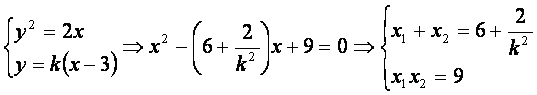
     综上，得“如果直线过点，那么＝”是真命题。

（2）（1）中命题的逆命题：在平面直角坐标系O中，直线与抛物线＝2

相交于、两点。如果 ＝，那么直线必过点。

       ∵设直线与轴的交点坐标为，则直线方程为，

把它代入得

      由，即直线必

过点。

      ∴（1）中命题的逆命题是假命题。