(17) (本小题满分12分)
已知函数![]() ,
,![]() .求:
.求:
(I)
函数![]() 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量![]() 的集合;
的集合;
(II)
函数![]() 的单调增区间.
的单调增区间.
(18) (本小题满分12分)
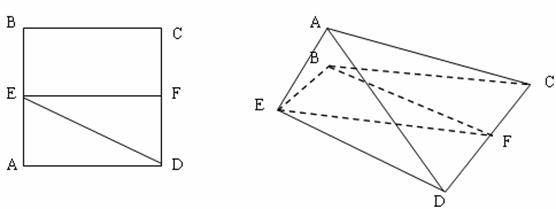
已知正方形![]() .
.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图
折起,如图
所示,记二面角![]() 的大小为
的大小为![]() .
.
(I)
证明![]() 平面
平面![]() ;
;
(II)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是
是
否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
(19) (本小题满分12分)
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、
1.17万元的概率分别为![]() 、
、![]() 、
、![]() ;已知乙项目的利润与产品价格的调整有关,在每
;已知乙项目的利润与产品价格的调整有关,在每
次调整中,价格下降的概率都是![]() ,设乙项目产品价格在一年内进行2次独立
,设乙项目产品价格在一年内进行2次独立
的调整,记乙项目产品价格在一年内的下降次数为![]() ,对乙项目每投资十万元,
,对乙项目每投资十万元,
![]() 取
取
0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量![]() 、
、![]() 分别
分别
表示对甲、乙两项目各投资十万元一年后的利润.
(I)
求![]() 、
、![]() 的概率分布和数学期望
的概率分布和数学期望![]() 、
、![]() ;
;
(II)
当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
(20) (本小题满分14分)
已知点![]() ,
,![]()
![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐
是坐
标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为
![]()
(I)
证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(II)当圆C的圆心到直线X-2Y=0的距离的最小值为时,求P的值。
21.(本小题满分12分)
已知函数f(x)=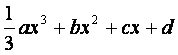 ,其中a
, b , c是以d为公差的等差数列,,
,其中a
, b , c是以d为公差的等差数列,,
且a>0,
d>0.设![]() [1-
[1-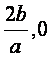 ]上,
]上,![]() 在
在![]() 处取得
处取得
最大值,在![]() ,将点
,将点![]() 依次记为A,
依次记为A,
B,
C.![]()
(I)求![]()
(II)若⊿ABC有一边平行于x轴,且面积为![]() ,求a
,d的值
,求a
,d的值
22.(本小题满分12分)
已知![]()
 ,其中
,其中![]() ,设
,设![]() ,
,![]() .
.
(I)
写出![]() ;
;
(II)
证明:对任意的![]() ,恒有
,恒有![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。