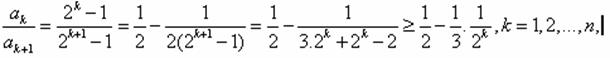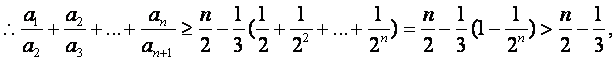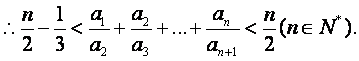三、解答题

（22）（本小题满分14分）

       已知数列满足

       （I）求数列的通项公式；

  　（II） 若数列｜b_n｜满足     ，

证明：｜b_n｜是等差数列

（Ⅲ）证明：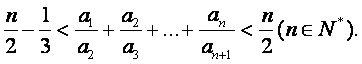

（22）本小题主要考查数列、不等式等基本知识，考查化归的数学思想方法，考查综合解题能力。满分14分。

       （I）解：

∵

       是以为首项，2为公比的等比数列。

       即　

       （II）证法一：

∵

       　　　　　　　　　　　　　①

       　　　　　　②

       ②－①，得

       即

　    ③－④，得　

       即　

       是等差数列。

       证法二：同证法一，得

       令得

       设下面用数学归纳法证明　

       （1）当时，等式成立。

       （2）假设当时，那么

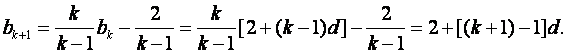
       这就是说，当时，等式也成立。

       根据（1）和（2），可知对任何都成立。

    ∵是等差数列。

       （III）证明：∵

    ∵
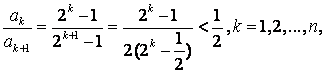