（21）（本题满分12分）

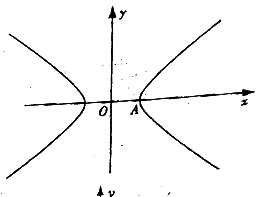
已知双曲线的中心在原点，右顶点为A（1，0）点P、Q在双

曲线的右支上，支M（m,0）到直线AP的距离为1。

（Ⅰ）若直线AP的斜率为k，且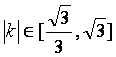，求实数m的

  取值范围；

（Ⅱ）当时，ΔAPQ的内心恰好是点M，求此双曲

线的方程。

解: (Ⅰ)由条件得直线AP的方程

  即

因为点M到直线AP的距离为1,

∵

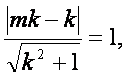
即.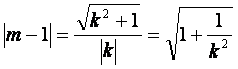

∵

∴

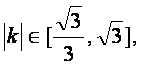
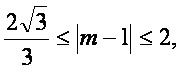
解得+1≤m≤3或--1≤m≤1--.

∴m的取值范围是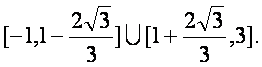

(Ⅱ)可设双曲线方程为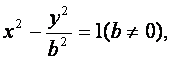

由

得.

又因为M是ΔAPQ的内心,M到AP的距离为1,所以∠MAP=45º,

直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1。因此，

（不妨设P在第一象限）

直线PQ方程为。

直线AP的方程y=x-1,

∴解得P的坐标是（2+，1+），将P点坐标代入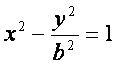得，

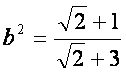
所以所求双曲线方程为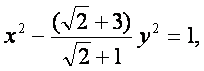

即