
三.解答题
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
我们把由半椭圆
![]() 与半椭圆
与半椭圆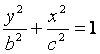
![]() 合成的曲线称作“果圆”,
合成的曲线称作“果圆”,
其中![]() ,
,![]() ,
,![]() .
.
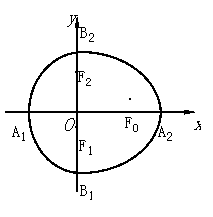 如图,点
如图,点![]() ,
,![]() ,
,![]() 是相应椭圆的焦点,
是相应椭圆的焦点,![]() ,
,![]() 和
和![]() ,
,![]() 分别是“果圆”与
分别是“果圆”与![]() ,
,![]() 轴的交点.
轴的交点.
(1)若![]() 是边长为1的等边三角形,求
是边长为1的等边三角形,求
“果圆”的方程;
(2)当![]()
![]()
![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)连接“果圆”上任意两点的线段称为“果圆”
的弦.试研究:是否存在实数![]() ,使斜率为
,使斜率为![]() 的“果圆”
的“果圆”
平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的![]() 值;
值;
若不存在,说明理由.
解:(1)![]()
 ,
,
![]() ,
,
于是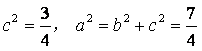 ,所求“果圆”方程为
,所求“果圆”方程为
![]() ,
, .
.
(2)由题意,得 ![]() ,即
,即![]() .
.
![]() ,
,![]() ,得
,得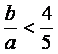 .
.
又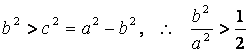 .
. 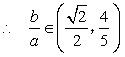 .
.
(3)设“果圆”![]() 的方程为
的方程为 ,
,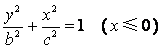 .
.
记平行弦的斜率为![]() .
.
当![]() 时,直线
时,直线![]() 与半椭圆
与半椭圆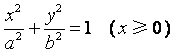 的交点是
的交点是
![]()
 ,与半椭圆
,与半椭圆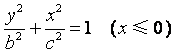 的交点是
的交点是![]()
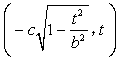 .
.
![]()
![]() 的中点
的中点![]()
![]() 满足
满足 
得  .
.
![]()
![]() ,
,![]()
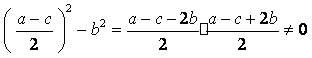 .
.
综上所述,当![]() 时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
当![]() 时,以
时,以![]() 为斜率过
为斜率过![]() 的直线
的直线![]() 与半椭圆
与半椭圆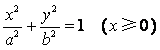 的交点
的交点
是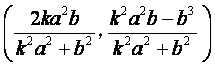 .
.
由此,在直线![]() 右侧,以
右侧,以![]() 为斜率的平行弦的中点轨迹在直线
为斜率的平行弦的中点轨迹在直线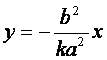 上,
上,
即不在某一椭圆上.
当![]() 时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。