三、解答题
(18)(本小题满分12分)
设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程![]()
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
解:(Ⅰ)由题意知:设基本事件空间为![]() ,记“方程
,记“方程![]() 没有实根”
没有实根”
为事件![]() ,“方程
,“方程![]() 有且仅有一个实根”为事件
有且仅有一个实根”为事件![]() ,“方程
,“方程![]()
有两个相异实数”为事件![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 是的基本事件总数为36个,
是的基本事件总数为36个,![]() 中的基本事件总数为17个,
中的基本事件总数为17个,![]() 中的基本事件
中的基本事件
总数为![]() 个,
个,![]() 中的基本事件总数为17个.
中的基本事件总数为17个.
又因为![]() 是互斥事件,
是互斥事件,
故所求概率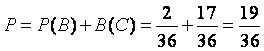 .
.
(Ⅱ)由题意,![]() 的可能取值为
的可能取值为![]() ,则
,则
![]() ,
,
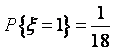 ,
,
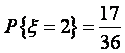 ,
,
故![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
所以![]() 的数学期望
的数学期望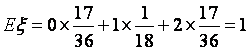 .
.
(Ⅲ)记“先后两次出现的点数有中5”为事件![]() ,“方程
,“方程![]() 有实数”
有实数”
为事件![]() ,由上面分析得
,由上面分析得
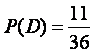 ,
,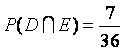 ,
,
 .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。