三、解答题
(22)(本小题满分12分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且方程
,且方程
![]()
有一根为![]()
(I)求![]()
(II)求![]() 的通项公式
的通项公式
解:
(Ⅰ)当n=1时,
![]()
有一根为![]() 于是
于是![]()
解得
![]() ……2分
……2分
当n=2时,
有一根为![]() 于是
于是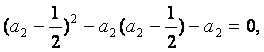
解得
![]() 。 ……5分
。 ……5分
(Ⅱ)由题设![]()
即
![]()
当![]()
![]() ①
①
由(Ⅰ)知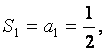
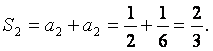
由①可得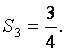
由此猜想
![]() ……8分
……8分
下面用数学归纳法证明这个结论。
(i)n=1时已知结论成立。
(ii)假设n=k时结论成立,即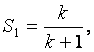
当n=k+1时,由①得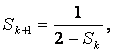
即
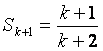 ,
,
故n=k+1时结论也成立。
综上,由(i)、(ii)可知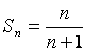 对所有正整数n都成立。 ……10分
对所有正整数n都成立。 ……10分
于是当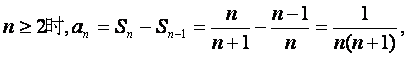
又n=1时,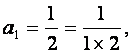 所以{
所以{![]() }的通项公式为
}的通项公式为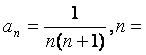 1,2,3,…。
1,2,3,…。
……12分
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。