三、解答题

19．(本小题满分12分)

    在锐角△ABC中，角A、B、C所对的边分别为a、b、c，已知sinA=，

    (1)求tan²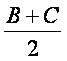+sin²的值；

    (2)若a=2，S_△ABC=，求b的值．

19.解：（1）因为锐角△ABC中，A+B+C=π，sinA=,所以cosA=

         则tan²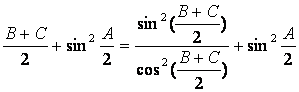

         =.

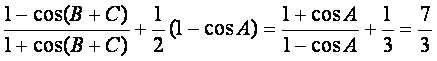
（2）因为S_△ABC=，又S_△ABC=bcsinA=bc·，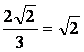

    则bc=3.将a=2,cosA=,c=代入余弦定理：a²=b²+c²-2bccosA,

    得b⁴-6b²+9=0,解得b=.