三、解答题
19.(本小题满分14分)
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比
数列{an2}各项的和为![]() 。
。
(Ⅰ)求数列{an}的首项a1和公比q:
(Ⅱ)对给定的k(k=1,2,…,n),设T{k}是首项为ak,公差为2ak-1的
等差数列,求数列T{2}的前10项之和:
(Ⅲ)设bi为数列![]() 的第i项,sn=b1+b2+…+bn,求sn,并求正整数
的第i项,sn=b1+b2+…+bn,求sn,并求正整数
m(m>1),使得![]()
![]() 存在且不等于零。
存在且不等于零。
(注:无穷等比数列各项的和即当n![]() 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)
解(Ⅰ)由题设可得:
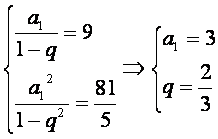
∴数列![]() 的首项
的首项![]() 为3,公比q为
为3,公比q为![]() .
.
(Ⅱ)由(Ⅰ)知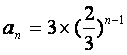 ,所以,等差数列
,所以,等差数列![]() 的的首项为
的的首项为![]() ,公差
,公差
![]()
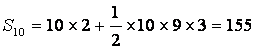 ,即数列
,即数列![]() 的前10项之和为155。
的前10项之和为155。
(Ⅲ)∵![]() 为数列
为数列![]() 的第i项,
的第i项,![]() 是首项为
是首项为![]() ,公差为2
,公差为2![]() -1的等差数列,
-1的等差数列,
∴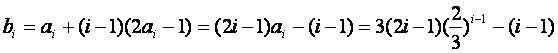
又![]()
=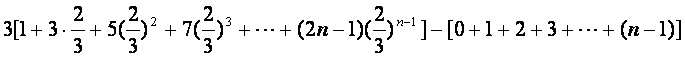
=
令
则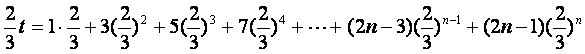
以上两式相减得: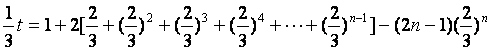

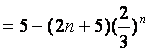
∴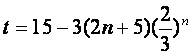
∴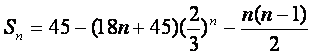
∴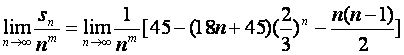
因为m>1,且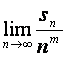 存在,
存在,
显然,当m=2时,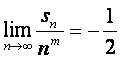 ,
,
当m>2时,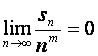 ,由题设
,由题设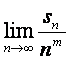 不等于0,因此m>2不合题意,
不等于0,因此m>2不合题意,
舍去。故满足题设的m的值为2。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。