解答题

17．（本题满分12分）

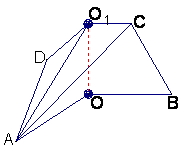
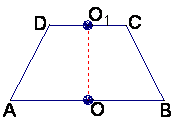
　  如图1，已知ABCD是上．下底边长分别为2和6，高为的等腰梯形，

    将它沿对称轴OO1折成直二面角，如图2.

　　（Ⅰ）证明：AC⊥BO1；

 （Ⅱ）求二面角O－AC－O1的大小.

                                                       图1

解法一（I）证明 由题设知OA⊥OO1，OB⊥OO1.

       所以∠AOB是所折成的直二面角的平面角，

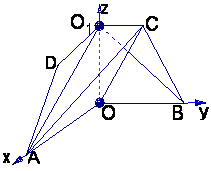
       即OA⊥OB. 故可以O为原点，OA、OB、OO1

              所在直线分别为轴、y轴、z轴建立空间直角坐标系，

       如图3，则相关各点的坐标是A（3，0，0），

       B（0，3，0），C（0，1，）

       O1（0，0，）.

       从而

     图3

       所以AC⊥BO1.                                

（II）解：因为所以BO1⊥OC，

由（I）AC⊥BO1，所以BO1⊥平面OAC，是平面OAC的一个法向量.

设是0平面O1AC的一个法向量，

由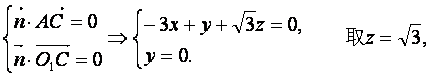    得.

设二面角O—AC—O1的大小为，由、的方向可知，>，

       所以cos，>=

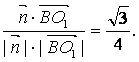
       即二面角O—AC—O1的大小是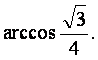

解法二（I）证明 由题设知OA⊥OO1，OB⊥OO1，

     所以∠AOB是所折成的直二面角的平面角，

       即OA⊥OB. 从而AO⊥平面OBCO1，

       OC是AC在面OBCO1内的射影.

       因为    ，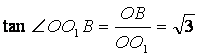

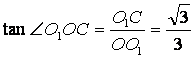       所以∠OO1B=60°，∠O1OC=30°，从而OC⊥BO1

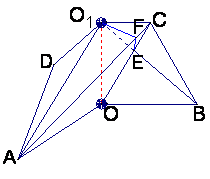       由三垂线定理得AC⊥BO1.

（II）解 由（I）AC⊥BO1，OC⊥BO1，知BO1⊥平面AOC.

       设OC∩O1B=E，过点E作EF⊥AC于F，连结O1F（如图4），则EF

       是O1F在平面AOC内的射影，由三垂线定理得O1F⊥AC.

       所以∠O1FE是二面角O—AC—O1的平面角.

       由题设知OA=3，OO1=，O1C=1，

       所以，

       从而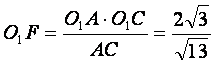，                                图4   

又O1E=OO1·sin30°=， 

       所以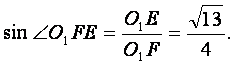  即二面角O—AC—O1的大小是