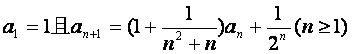解答题

22．（本小题满分12分）

       数列{an}满足.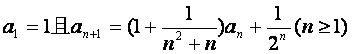

    （Ⅰ）用数学归纳法证明：；

  （Ⅱ）已知不等式，其中无理数

e=2.71828….

（Ⅰ）证明：（1）当n=2时，，不等式成立.

           （2）假设当时不等式成立，即

那么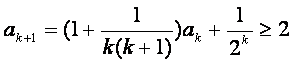.  这就是说，当时不等式成立.

根据（1）、（2）可知：成立.

（Ⅱ）证法一：

由递推公式及（Ⅰ）的结论有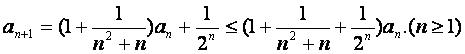

两边取对数并利用已知不等式得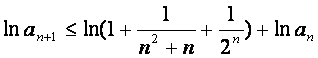

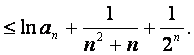  故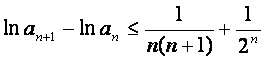 

上式从1到求和可得

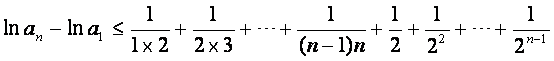
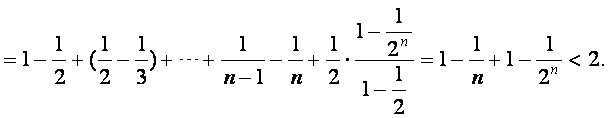
即

（Ⅱ）证法二：

由数学归纳法易证成立，故

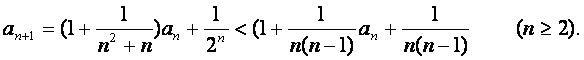
令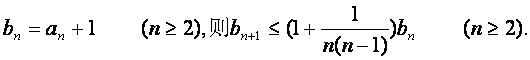

取对数并利用已知不等式得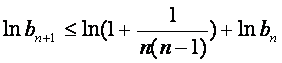 

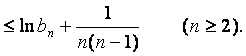
上式从2到n求和得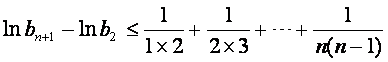 

因

故成立.