选择题(每小题5分)
(8)函数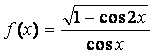
(A)在[0，
)，(
，
]上递增，在[，
)，(
，2
]上递减
(B)在[0，
)，[
，
)上递增，在(，
]，(，2
]上递减
(C)在(
，]，(，2
]上递增，在[0，)，[
，)上递减
(D)在[，)，(
，2]上递增，在[0，)，(
，]上递减
填空题(每小题5分)
(13) 对于函数
定义域中任意的
(
)，有如下结论：
①
；
②
；
③
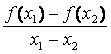>0；
④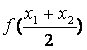
<
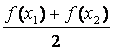
当
时，上述结论中正确结论的序号是
解答题
15 （本小题共13分）
已知函数
(I)求
的单调递减区间；
(Ⅱ)若
在区间[一2，2]上的最大值为20，求它在该区间上的最小值
20 （本小题共14分）
设
是定义在[0，1]上的函数，若存在
，使得在[0，
]上
单调递增，在[
，1]单调递减，则称为[0，1]上的单峰函数，为峰点，
包含峰点的区间为含峰区间
对任意的[0，1]上的单峰函数
，下面研究缩短其含峰区间长度的方法
（Ⅰ）证明：对任意的
, 
,若
，则（0，
）为
含峰区间；若
，则（
，1）为含峰区间；
（Ⅱ）对给定的
（0<
<0.5），证明：存在
,满足
，
使得由（Ⅰ）确定的含峰区间的长度不大于0.5+;
(Ⅲ)选取
,
由（Ⅰ）可确定含峰区间为（0，
）或（，1），
在所得的含峰区间内选取
,由
与
或与
类似地可确定是一个新的含峰区间．
在第一次确定的含峰区间为（0，
）的情况下，试确定
的值，满足两两
之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34
（区间长度等于区间的右端点与左端点之差）
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。