解答题
(21)(本题满分12分)
已知a为实数,![]()
(Ⅰ)求导数![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 在[--2,2]
上的最大值和最小值;
在[--2,2]
上的最大值和最小值;
(Ⅲ)若![]() 在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
解:
(Ⅰ)由原式得![]()
∴![]()
(Ⅱ)由![]() 得
得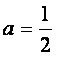 ,此时有
,此时有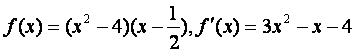 .
.
由![]() 得
得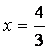 或x=-1
, 又
或x=-1
, 又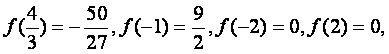
所以f(x)在[--2,2]上的最大值为![]() 最小值为
最小值为![]()
(Ⅲ)解法一:
![]() 的图象为开口向上且过点(0,--4)的抛物线,
的图象为开口向上且过点(0,--4)的抛物线,
由条件得
![]()
即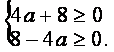 ∴--2≤a≤2.
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令![]() 即
即![]() 由求根公式得:
由求根公式得:
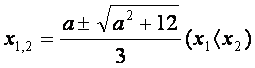
所以![]() 在
在![]() 和
和![]() 上非负.
上非负.
由题意可知,当x≤-2或x≥2时,
![]() ≥0,
≥0,
从而x1≥-2, x2≤2,
即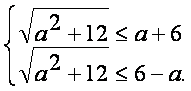 解不等式组得:
--2≤a≤2.
解不等式组得:
--2≤a≤2.
∴a的取值范围是[--2,2].
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。