解答题

22.（本小题满分14分）

椭圆的中心是原点O，它的短轴长为，相应于焦点的

准线与轴相交于点A，，过点A的直线与椭圆相交于P、Q两点。

（1）求椭圆的方程及离心率；（2）若，求直线PQ的方程。

本小题主要考查椭圆的标准方程和几何性质，直线方程，平面向量的计算，

曲线和方程的关系等解析几何的基本思想方法和综合解题能力，满分14分。

（1）解：由题意，可设椭圆的方程为 

         由已知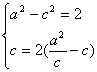得    解得，

所以椭圆的方程为，离心率

（2）解：由（1）可得，设直线PQ的方程为，由方程组

            得

依题意，得

设，

则     ①           ②

由直线PQ的方程得，

于是     ③

∵      ∴       ④

由①②③④得，从而

所以直线PQ的方程为或