解答题
21. (本小题满分12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]() ,其中a为常数,k为非零常数。
,其中a为常数,k为非零常数。
(1)令![]()
![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)当![]() 时,求
时,求![]() 。
。
本小题主要考查函数、数列、等比数列和极限等概念,考查灵活应用
数学知识分析问题和解决问题的能力,满分12分。
(1)证明:由![]() ,可得
,可得
![]() 。
。
由数学归纳法可证![]()
![]() 。
。
由题设条件,当![]() 时
时
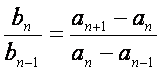
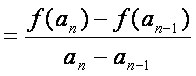
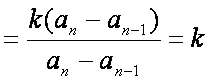
因此,数列![]() 是一个公比为k的等比数列。
是一个公比为k的等比数列。
(2)解:由(1)知,![]()
当![]() 时,
时,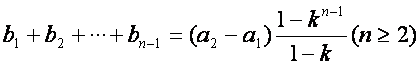
当![]() 时,
时,![]()
![]() 。
。
而![]()
![]()
所以,当![]() 时
时
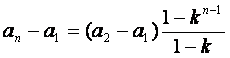
![]() 。
。
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
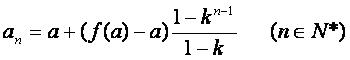
当![]() 时
时
![]()
![]() 。
。
上式对![]() 也成立,所以,数列
也成立,所以,数列![]() 的通项公式为
的通项公式为
![]()
![]() ,
,
(2)解:当![]() 时
时
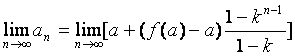
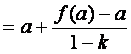
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。