解答题
22.(本小题满分14分)
给定抛物线C:![]() F是C的焦点,过点F的直线
F是C的焦点,过点F的直线![]() 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设![]() 的斜率为1,求
的斜率为1,求![]() 夹角的大小;
夹角的大小;
(Ⅱ)设![]() ,求
,求![]() 在
在![]() 轴上截距的变化范围.
轴上截距的变化范围.
本小题主要考查抛物线的性质,直线与抛物线的关系以及解析几何的基本方法、
思想和综合解题能力。满分14分。
解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为![]()
将![]() 代入方程
代入方程![]() ,并整理得
,并整理得
![]()
设![]() 则有
则有
![]()
![]()
![]()
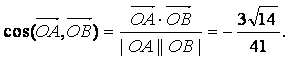
所以![]() 夹角的大小为
夹角的大小为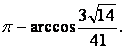
(Ⅱ)由题设![]() 得
得
![]()
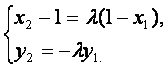
由②得![]() ,
∵
,
∵
![]() ∴
∴![]() ③
③
联立①、③解得![]() ,依题意有
,依题意有![]()
∴![]() 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为
![]()
当![]() 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为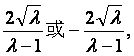
由
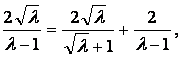 可知
可知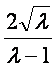 在[4,9]上是递减的,
在[4,9]上是递减的,
∴
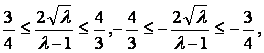
直线l在y轴上截距的变化范围为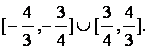
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。