解答题

（22）（本小题满分14分）

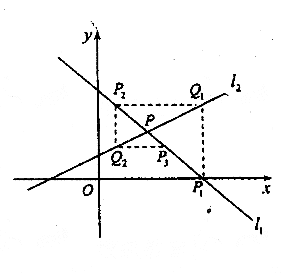
如图，直线与相交于点P。直线

与x轴交于点P₁，过点P₁作x轴的垂线交直线于点Q₁，过点Q₁作y轴的

垂线交直线于点P₂，过点P₂作x轴的垂线交直线于点Q₂，…，这样

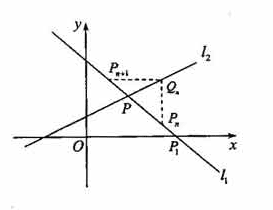
一直作下去，可得到一系列点P₁，Q₁，P₂，Q₂，…。点P_n（n=1,2,…）

的横坐标构成数列。

  (Ⅰ)证明

(Ⅱ)求数列的通项公式；

(Ⅲ)比较与的大小。

 解:

 (Ⅰ)证明  设点的坐标是由已知条件得

点的坐标分别是：

由在直线上，

得

所以

即

(Ⅱ)解 由题设知 又由（Ⅰ）知

所以 数列是首项为x₁—1 ,公比为的等比数列。

从而即，。

(Ⅲ) 解  由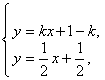得点P的坐标为（1，1）。

所以

（当，即或时，

   而此时0所以故

当0 即时，

而此时所以故